题目内容
直角三角形的两条直角边长为5和12，则它的外接圆周长为________，内切圆面积为________．
13π 4π
分析：连接AO、BO、CO，过O作OD⊥AC于D，OF⊥AB于F，OE⊥BC于E，设OE=OD=OF=r，根据勾股定理求出AB，得到三角形的外接圆的半径，根据三角形的面积公式得出
×5×12=×5×r+×BC×r+×13×r，求出即可．
解答：
解：
O为△ABC内切圆的圆心，Q为△ABC外接圆的圆心，
由勾股定理得：AB=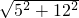
=13，
∴△ABC的外接圆的半径是×13=
，周长是2π×=13π，
连接AO、BO、CO，过O作OD⊥AC于D，OF⊥AB于F，OE⊥BC于E，
则设OE=OD=OF=r，
根据三角形的面积公式得：S△ABC=S△ACO+S△BCO+S△ABO，
∴×5×12=×5×r+×BC×r+×13×r，
解得：r=2，
∴内切圆的面积是π×22=4π．
故答案为：13π，4π．
点评：本题主要考查对勾股定理，三角形的外接圆与外心，三角形的内切圆与内心，三角形的面积等知识点的理解和掌握，能熟练地运用性质进行推理和计算是解此题的关键．
分析：连接AO、BO、CO，过O作OD⊥AC于D，OF⊥AB于F，OE⊥BC于E，设OE=OD=OF=r，根据勾股定理求出AB，得到三角形的外接圆的半径，根据三角形的面积公式得出
×5×12=×5×r+×BC×r+×13×r，求出即可．解答：
解：O为△ABC内切圆的圆心，Q为△ABC外接圆的圆心，
由勾股定理得：AB=
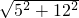=13，∴△ABC的外接圆的半径是
×13=，周长是2π×=13π，连接AO、BO、CO，过O作OD⊥AC于D，OF⊥AB于F，OE⊥BC于E，
则设OE=OD=OF=r，
根据三角形的面积公式得：S△ABC=S△ACO+S△BCO+S△ABO，
∴
×5×12=×5×r+×BC×r+×13×r，解得：r=2，
∴内切圆的面积是π×22=4π．
故答案为：13π，4π．
点评：本题主要考查对勾股定理，三角形的外接圆与外心，三角形的内切圆与内心，三角形的面积等知识点的理解和掌握，能熟练地运用性质进行推理和计算是解此题的关键．
练习册系列答案
相关题目
