题目内容
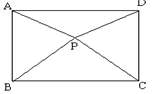
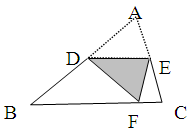
如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连结AP交BC于点E,连结BP交AC于点F.

(1)试说明∠CAE=∠CBF;
(2)AE和BF 是否相等?请说明理由.

(1)试说明∠CAE=∠CBF;
(2)AE和BF 是否相等?请说明理由.
(1) ∵△ 是等腰△,
是等腰△, 是底边上的高线,∴
是底边上的高线,∴ ,
,
又∵ , ∴△
, ∴△ ≌△
≌△ ∴
∴ , 即
, 即 --- 5分
--- 5分
(2) ∵ ,
,  ,
, ,
,
∴△ ≌△
≌△ ,∴
,∴ . --- 5分
. --- 5分
 是等腰△,
是等腰△, 是底边上的高线,∴
是底边上的高线,∴ ,
,又∵
 , ∴△
, ∴△ ≌△
≌△ ∴
∴ , 即
, 即 --- 5分
--- 5分(2) ∵
 ,
,  ,
, ,
,∴△
 ≌△
≌△ ,∴
,∴ . --- 5分
. --- 5分(1)根据等腰三角形三线合一的性质可得CH平分∠ACB,再证明△ACE和△BCF全等,然后根据全等三角形对应角相等可得结论;
(2)证明△AEC≌△BFC,根据全等三角形对应边相等即可证明.
(2)证明△AEC≌△BFC,根据全等三角形对应边相等即可证明.

练习册系列答案
相关题目
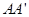 、
、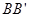 的中点O连在一起,使
的中点O连在一起,使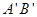 的长等于内槽宽AB,那么判定△AOB
的长等于内槽宽AB,那么判定△AOB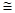 △
△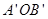 的理由是( )
的理由是( )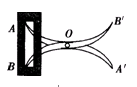
 .
.