Question

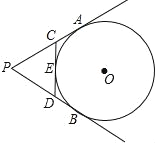
【题目】如图，已知PA、PB切⊙O于A、B两点，CD切⊙O于E，△PCD的周长为20，sin∠APB＝，则⊙O的半径( )

A. 4B. 5C. 6D. 7

Answer 1

【答案】B

【解析】

连接OA、OB、OP，延长BO交PA的延长线于点F．已知PA，PB切⊙O于A、B两点，CD切⊙O于点E,根据切线的性质定理及切线长定理可得∴∠OAF＝∠PBF＝90°，CA＝CE，DB＝DE，PA＝PB，由△PCD的周长＝PC+CE+DE+PD＝PC+AC+PD+DB＝PA+PB＝20，可求得PA＝PB＝10，由sin∠APB＝可得sin∠PFB==，即=，即可求得AF＝，在Rt△AOF中，由tan∠AOF=tan∠BPF==即可求得OA的长.

连接OA、OB、OP，延长BO交PA的延长线于点F．

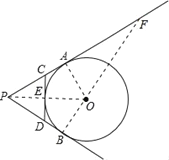
∵PA，PB切⊙O于A、B两点，CD切⊙O于点E

∴∠OAF＝∠PBF＝90°，CA＝CE，DB＝DE，PA＝PB，

∵△PCD的周长＝PC+CE+DE+PD＝PC+AC+PD+DB＝PA+PB＝20，

∴PA＝PB＝10，

∵sin∠APB＝，

∴sin∠PFB==，

∴=，

解得：AF＝，

在Rt△AOF中，tan∠AOF=tan∠BPF==，

∴，

∴OA＝5，

故选B．