Question

如图，已知AB∥CD，C在D的右侧，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E．∠ADC=70°.

（1）求∠EDC的度数；
（2）若∠ABC=n°，求∠BED的度数（用含n的代数式表示）；
（3）将线段BC沿DC方向平移， 使得点B在点A的右侧，其他条件不变，若∠ABC=n°，求∠BED的度数（用含n的代数式表示）．

Answer 1

（1）35°；（2）n°+35°；（3）215°-n°.

试题分析：（1）根据角平分线的性质结合∠ADC=70°即可求得结果；
（2）过点E作EF∥AB，即可得到AB∥CD∥EF，从而可得∠ABE=∠BEF，∠CDE=∠DEF，再根据角平分线的性质可得∠ABE=∠ABC=n°，∠CDE=∠ADC=35°，即可求得结果；
（3）过点E作EF∥AB，根据角平分线的性质可得∠ABE=∠ABC=n°，∠CDE=∠ADC=35°，再根据平行线的性质可得∠BEF的度数，从而求得结果.
（1）∵DE平分∠ADC，∠ADC=70°，
∴∠EDC=∠ADC=×70°=35°；
（2）过点E作EF∥AB，

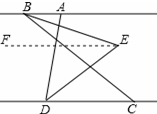
∵AB∥CD，
∴AB∥CD∥EF，
∴∠ABE=∠BEF，∠CDE=∠DEF，
∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=70°，
∴∠ABE=∠ABC=n°，∠CDE=∠ADC=35°，
∴∠BED=∠BEF+∠DEF=n°+35°；
（3）过点E作EF∥AB

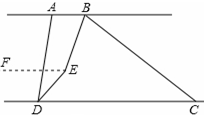
∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=80°
∴∠ABE=∠ABC=n°，∠CDE=∠ADC=35°
∵AB∥CD，
∴AB∥CD∥EF，
∴∠BEF=180°-∠ABE=180°-n°，∠CDE=∠DEF=35°，
∴∠BED=∠BEF+∠DEF=180°-n°+35°=215°-n°.
点评：本题知识点较多，综合性强，难度较大，是中考常见题，正确作出辅助线是解题关键.