题目内容
如图,在△ABC中,AD⊥BC于D,点D,E,F分别是BC,AB,AC的中点.求证:四边形AEDF是菱形.

证明见解析
证明:∵点D,E,F分别是BC,AB,AC的中点,∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形。
又∵AD⊥BC,BD=CD,∴AB=AC。∴AE=AF。
∴平行四边形AEDF是菱形。
首先判定四边形AEDF是平行四边形,然后证得AE=AF,利用邻边相等的平行四边形是菱形判定菱形即可。
∴四边形AEDF是平行四边形。
又∵AD⊥BC,BD=CD,∴AB=AC。∴AE=AF。
∴平行四边形AEDF是菱形。
首先判定四边形AEDF是平行四边形,然后证得AE=AF,利用邻边相等的平行四边形是菱形判定菱形即可。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目

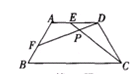

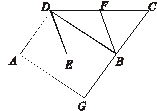
 和19
和19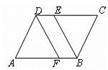
 沿EF折叠,使点
沿EF折叠,使点 落在
落在 边上的点B处;沿BG折叠,使点
边上的点B处;沿BG折叠,使点 落在点D处,且BD过F点.
落在点D处,且BD过F点.
