题目内容
 如图,扇形OAB的半径为10cm,∠AOB=90°,分别以OA、OB为直径作半圆,两半圆交于点C,则图中阴影部分的面积为
如图,扇形OAB的半径为10cm,∠AOB=90°,分别以OA、OB为直径作半圆,两半圆交于点C,则图中阴影部分的面积为分析:设OA的中点是D,则∠CDO=90度,这样就可以求出弧OC与弦OC围成的弓形的面积,则两个圆的弧OC围成的阴影部分的面积.用扇形OAB的面积减去两个半圆的面积,加上两个弧OC围成的面积的2倍就是阴影部分的面积.
解答: 解:设OA的中点是D,则∠CDO=90°,
解:设OA的中点是D,则∠CDO=90°,
S扇形OAB=
×π×102=25πcm2,
S半圆OAC=
×π×52=
πcm2,
S△ODC=
×5×5=
cm2,
S弧OC=
S半圆OAC-S△ODC=(
π-
)cm2,
∴25π-
π×2+(
π-
)×4=
-25cm2;
即图中阴影部分的面积为25π-50cm2.
 解:设OA的中点是D,则∠CDO=90°,
解:设OA的中点是D,则∠CDO=90°,S扇形OAB=
| 1 |
| 4 |
S半圆OAC=
| 1 |
| 2 |
| 25 |
| 2 |
S△ODC=
| 1 |
| 2 |
| 25 |
| 2 |
S弧OC=
| 1 |
| 2 |
| 25 |
| 4 |
| 25 |
| 2 |
∴25π-
| 25 |
| 2 |
| 25 |
| 4 |
| 25 |
| 2 |
| 25π |
| 2 |
即图中阴影部分的面积为25π-50cm2.
点评:不规则图形的面积可以转化为几个不规则的图形的面积的和或差的计算.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 是
是
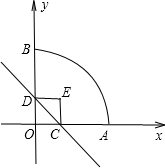
 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则: 是______;
是______; 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积. 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.
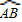 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.