题目内容
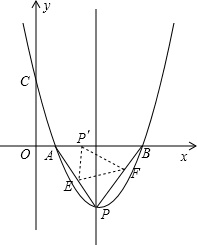 已知:抛物线经过A(2,0)、B(8,0)、C(0,
已知:抛物线经过A(2,0)、B(8,0)、C(0,16
| ||
| 3 |
(1)求:抛物线的解析式;
(2)设抛物线的顶点为P,把△APB翻折,使点P落在线段AB上(不与A、B重合),记作P′,折痕为EF,设AP′=x,PE=y,求y关于x的函数关系式,并写出定义域;
(3)当点P′在线段AB上运动但不与A、B重合时,能否使△EFP′的一边与x轴垂直?若能,请求出此时点P′的坐标;若不能,请你说明理由.
分析:(1)设抛物线的解析式为y=a(x-2)(x-8)将C点坐标代入即可求得抛物线的解析式;
(2)先求出P点坐标,在Rt△P′EG中,根据勾股定理便可求出y关于x的函数关系式;
(3)分别令EP′⊥x轴、FP′⊥x轴、EF⊥x轴进行分类讨论,便可得出满足题意得P点坐标.
(2)先求出P点坐标,在Rt△P′EG中,根据勾股定理便可求出y关于x的函数关系式;
(3)分别令EP′⊥x轴、FP′⊥x轴、EF⊥x轴进行分类讨论,便可得出满足题意得P点坐标.
解答:解:(1)设抛物线的解析式为y=a(x-2)(x-8)(1分)
把(0,
)代入得a=
(1分)
∴y=
(x-2)(x-8)
即y=
x2-
x+
(2分)
(2)顶点P(5,-3
)
AP=AB=BP=6(1分)
∴∠PAP′=60°(1分)
作P′G⊥AP于G,
则AG=
x,P′G=
x
又P′E=PE=y,EG=6-
x-y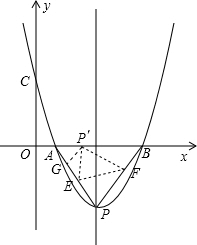
在Rt△P′EG中,(
x)2+(6-
x-y)2=y2(2分)
∴y=
(0<x<6)(2分)
(3)①若EP′⊥x轴,则6-y=2x,6-
=2x,
x1=12-6
,x2=12+6
(舍去)(1分)
∴P′(14-6
,0)
②若FP′⊥x轴,则6-y=
x,6-
=
x,
x3=6
-6,x4=-6
-6(舍去)(1分)
∴P′(6
-4,0)
③若EF⊥x轴,显然不可能.
∴P′(14-6
,0)或P′(6
-4,0)(1分)
把(0,
16
| ||
| 3 |
| ||
| 3 |
∴y=
| ||
| 3 |
即y=
| ||
| 3 |
10
| ||
| 3 |
16
| ||
| 3 |
(2)顶点P(5,-3
| 3 |
AP=AB=BP=6(1分)
∴∠PAP′=60°(1分)
作P′G⊥AP于G,
则AG=
| 1 |
| 2 |
| ||
| 2 |
又P′E=PE=y,EG=6-
| 1 |
| 2 |

在Rt△P′EG中,(
| ||
| 2 |
| 1 |
| 2 |
∴y=
| x2-6x+36 |
| 12-x |
(3)①若EP′⊥x轴,则6-y=2x,6-
| x2-6x+36 |
| 12-x |
x1=12-6
| 3 |
| 3 |
∴P′(14-6
| 3 |
②若FP′⊥x轴,则6-y=
| 1 |
| 2 |
| x2-6x+36 |
| 12-x |
| 1 |
| 2 |
x3=6
| 3 |
| 3 |
∴P′(6
| 3 |
③若EF⊥x轴,显然不可能.
∴P′(14-6
| 3 |
| 3 |
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和勾股定理等知识点,是各地中考的热点和难点,解题时注意数形结合和分类讨论等数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
相关题目
 且与x轴的另一个交点为E.
且与x轴的另一个交点为E.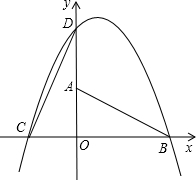 ,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.
,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.