题目内容
 已知二次函数
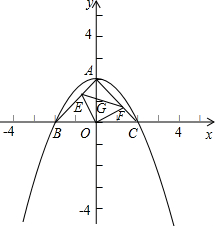
已知二次函数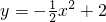 的图象与x轴交于B,C两点(点B在点C的左边),与y轴交于点A,E,F分别是线段AB,AC上的点,且OE⊥OF
的图象与x轴交于B,C两点(点B在点C的左边),与y轴交于点A,E,F分别是线段AB,AC上的点,且OE⊥OF
(1)求A,B,C三点的坐标
(2)猜测△EOF是什么三角形,并证明你的猜测
(3)若EF与OA交于点G,试探究∠AEO与∠AGF的关系,结论:∠AEO______∠AGF(填上>,<,=),并请证明
(4)当点E,F分别在线段AB,AC上运动时,四边形AEOF的面积是否发生变化?若不变,请说明理由,若变化,请求其值的变化范围.
解:(1)令x=0得y=2,∴A(0,2)
令y=0得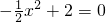 ,
,
解得x=±2,
∴B(-2,0),C(2,0)
(2)猜测△EOF是等腰直角三角形
证明:∵A(0,2),B(-2,0),C(2,0),
∴OA=OB=OC=2,BC=4,由勾股定理可以求出AB=BC=2 ,
,
∴BC2=AB2+AC2
∴△ABC是直角三角形,
∵AB=BC,
∴△ABC是等腰直角三角形
∴∠BAC=90°,∠OBA=∠OCA=45°
同理∠OCA=∠OAC=45°
∴∠OAB=∠OCA=45°
∵OE⊥OF
∴∠EOF=90°,即∠AOE+∠AOF=90°,
∵∠AOF+∠FOC=90°
∴∠AOE=∠FOC
∴△EOA≌△FOC,
∴OE=OF,
∴△EOF是等腰直角三角形.
(3)∠AEO=∠AGF
证明:∵△EOF是等腰直角三角形
∴∠OEF=45°,
∵∠BAO=45°,
∴∠OEF=∠BAO,
∵AGF=∠BAO+∠AEG,∠AEO=∠AEG+∠OEF,
∴∠BAO+∠AEG=∠AEG+∠OEF,
即∠AEO=∠AGF
故答案为:=.
( 4 ) 四边形AEOF的面积不会发生变化.
证明:∵△AOE≌△COF,
∴S△AOE=S△COF,
∵S四边形EOFA=S△AOE+S△AOF
∴S四边形EOFA=S△AOF+S△OFC,
∴S四边形EOFA=S△AOC,
∵S△AOC是定值
∴当点E,F运动时,四边形AEOF的面积不发生变化.
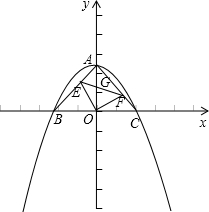
分析:(1)当x=0时,求出y的值就可以求出A点的坐标,当y=0时,求出x的值就可以求出点B、C的坐标.
(2)由(1)的结论可以求出OA、OB、OC、AB、AC的长度,由勾股定理的逆定理可以证明△ABC是等腰直角三角形,进而可以证明△OEA≌△OFC,从而证明△EOF是等腰直角三角形.
(3)由(2)的结论外角与内角的关系可以得出∠AEO=∠OEF+∠AEG与∠AGF=∠BAG+∠AEG,再由∠BAO=∠OEF=45°,从而可以得出∠AEO与∠AGF的大小关系.
(4)由(2)可知△EOA≌△FOC,可以得出S△EOA=S△FOC,则四边形AEOF的面积就等于S△AOC的面积.从而得出结论.
点评:本题是一道二次函数的综合试题,考查了二次函数图象上的点的坐标的特征,全等三角形的判定与性质,等腰直角三角形的性质及勾股定理的运用.
令y=0得
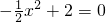 ,
,解得x=±2,
∴B(-2,0),C(2,0)
(2)猜测△EOF是等腰直角三角形
证明:∵A(0,2),B(-2,0),C(2,0),
∴OA=OB=OC=2,BC=4,由勾股定理可以求出AB=BC=2
 ,
,∴BC2=AB2+AC2
∴△ABC是直角三角形,
∵AB=BC,
∴△ABC是等腰直角三角形
∴∠BAC=90°,∠OBA=∠OCA=45°
同理∠OCA=∠OAC=45°
∴∠OAB=∠OCA=45°
∵OE⊥OF
∴∠EOF=90°,即∠AOE+∠AOF=90°,
∵∠AOF+∠FOC=90°
∴∠AOE=∠FOC
∴△EOA≌△FOC,
∴OE=OF,
∴△EOF是等腰直角三角形.
(3)∠AEO=∠AGF
证明:∵△EOF是等腰直角三角形
∴∠OEF=45°,
∵∠BAO=45°,
∴∠OEF=∠BAO,
∵AGF=∠BAO+∠AEG,∠AEO=∠AEG+∠OEF,
∴∠BAO+∠AEG=∠AEG+∠OEF,
即∠AEO=∠AGF
故答案为:=.
( 4 ) 四边形AEOF的面积不会发生变化.
证明:∵△AOE≌△COF,
∴S△AOE=S△COF,
∵S四边形EOFA=S△AOE+S△AOF
∴S四边形EOFA=S△AOF+S△OFC,
∴S四边形EOFA=S△AOC,
∵S△AOC是定值
∴当点E,F运动时,四边形AEOF的面积不发生变化.

分析:(1)当x=0时,求出y的值就可以求出A点的坐标,当y=0时,求出x的值就可以求出点B、C的坐标.
(2)由(1)的结论可以求出OA、OB、OC、AB、AC的长度,由勾股定理的逆定理可以证明△ABC是等腰直角三角形,进而可以证明△OEA≌△OFC,从而证明△EOF是等腰直角三角形.
(3)由(2)的结论外角与内角的关系可以得出∠AEO=∠OEF+∠AEG与∠AGF=∠BAG+∠AEG,再由∠BAO=∠OEF=45°,从而可以得出∠AEO与∠AGF的大小关系.
(4)由(2)可知△EOA≌△FOC,可以得出S△EOA=S△FOC,则四边形AEOF的面积就等于S△AOC的面积.从而得出结论.
点评:本题是一道二次函数的综合试题,考查了二次函数图象上的点的坐标的特征,全等三角形的判定与性质,等腰直角三角形的性质及勾股定理的运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知二次函数的图象与y轴的交点坐标为(0,a),与x轴的交点坐标为(b,0)和(-b,0),若a>0,则函数解析式为( )
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
 已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.
已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.