题目内容
（2008•昆明）如图，在Rt△ABC中，∠A=90°，AC=6cm，AB=8cm，把AB边翻折，使AB边落在BC边上，点A落在点E处，折痕为BD，则sin∠DBE的值为（ ）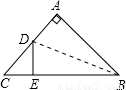
A．
B．
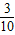
C．
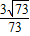
D．
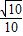
【答案】分析：解：根据折叠的性质，利用三角形的面积求出AD的长，再利用勾股定理即可求出BD的长，问题也就解决了．
解答：解：根据折叠的含义可以知道：△ABD≌△EBD，则AD=DE=x，
在直角△ABC中利用勾股定理解得：BC=10，S△ABC=SABD+S△BCD，
即：
AB•AD+
BC•DE=
AB•AC则8x+10x=48，
解得：x=
．
在直角△ABD中，BD=
=
=
，
因而：sin∠DBE=sin∠ABD=
．
故选D．
点评：已知折叠问题就是已知图形的全等，并且三角函数值只与角的大小有关，因而求一个角的函数值，可以转化为求与它相等的其它角的三角函数值．
解答：解：根据折叠的含义可以知道：△ABD≌△EBD，则AD=DE=x，
在直角△ABC中利用勾股定理解得：BC=10，S△ABC=SABD+S△BCD，
即：
AB•AD+BC•DE=AB•AC则8x+10x=48，解得：x=
．在直角△ABD中，BD=
==，因而：sin∠DBE=sin∠ABD=
．故选D．
点评：已知折叠问题就是已知图形的全等，并且三角函数值只与角的大小有关，因而求一个角的函数值，可以转化为求与它相等的其它角的三角函数值．
练习册系列答案
孟建平名校考卷系列答案
相关题目
：3？若存在，请求出此时点P的坐标；若不存在，请说明理由．（注意：本题中的结果均保留根号）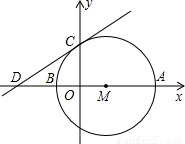
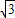：3？若存在，请求出此时点P的坐标；若不存在，请说明理由．（注意：本题中的结果均保留根号）
