题目内容
(3分)下列运用等式性质,变形错误的是( )
A. 如果a=b,那么a+c=b+c B. 如果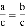 ,那么a=b
,那么a=b
C. 如果a=b,那么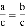 D. 如果a2=2a,那么a=2
D. 如果a2=2a,那么a=2
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
题目内容
(3分)下列运用等式性质,变形错误的是( )
A. 如果a=b,那么a+c=b+c B. 如果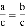 ,那么a=b
,那么a=b
C. 如果a=b,那么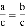 D. 如果a2=2a,那么a=2
D. 如果a2=2a,那么a=2
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案