题目内容
(2003•常州)一元二次方程y2+2y-4=0的根的情况是( )A.有两个相等的实数根
B.有两个不相等的实数根,且两根同号
C.有两个不相等的实数根,且两根异号
D.没有实数根
【答案】分析:判断一元二次方程的根的情况,只要看方程根的判别式△=b2-4ac的值的符号就可以了.
解答:解:∵a=1,b=2,c=-4,
∴△=b2-4ac
=22-4×1×(-4)
=20>0,
而y1•y2=-4,
∴有两个不相等的实数根,且两根异号.
故选C.
点评:总结一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
解答:解:∵a=1,b=2,c=-4,
∴△=b2-4ac
=22-4×1×(-4)
=20>0,
而y1•y2=-4,
∴有两个不相等的实数根,且两根异号.
故选C.
点评:总结一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
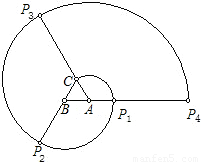
(2003•常州)如图,正三角形ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4….设ln为扇形Dn的弧长(n=1,2,3…),回答下列问题:
(1)按照要求填表:
(2)根据上表所反映的规律,试估计n至少为何值时,扇形Dn的弧长能绕地球赤道一周(设地球赤道半径为6400km).
(1)按照要求填表:
| n | 1 | 2 | 3 | 4 |
| ln |

(2003•常州)如图,正三角形ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4….设ln为扇形Dn的弧长(n=1,2,3…),回答下列问题:
(1)按照要求填表:
(2)根据上表所反映的规律,试估计n至少为何值时,扇形Dn的弧长能绕地球赤道一周(设地球赤道半径为6400km).

(1)按照要求填表:
| n | 1 | 2 | 3 | 4 |
| ln |

(2003•常州)甲、乙两个班的学生到超市上购买苹果,苹果的价格如下:
甲班分两次共购买苹果70千克(第二次多于第一次),共付出189元,乙班则一次购买苹果70千克.
(1)乙班比甲班少付出多少元?
(2)甲班第一次、第二次分别购买苹果多少千克?
| 购苹果数 | 不超过30kg | 30kg以上但不超过50kg | 50kg以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
(1)乙班比甲班少付出多少元?
(2)甲班第一次、第二次分别购买苹果多少千克?