题目内容
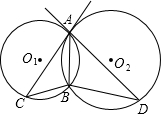如图，⊙O1与⊙O2相交于A、B两点，AC是⊙O2的切线，AD是⊙O1的切线，若BC=4，BD=9，则AB的长为
- A.5
- B.6
- C.7
- D.8
B
分析：由题易证△ABC∽△DBA，因而得出
=
求解．
解答：∵AC是⊙O2的切线，AD是⊙O1的切线，
∴∠CAB=∠D，∠DAB=∠C，
∴△ABC∽△DBA，
∴=，
则
=
，解得：AB=6．
故选B．
点评：本题利用了弦切角定理，从而得到三角形相似，根据相似三角形的对应边的比相等就可以求出线段的长．
分析：由题易证△ABC∽△DBA，因而得出
=求解．解答：∵AC是⊙O2的切线，AD是⊙O1的切线，
∴∠CAB=∠D，∠DAB=∠C，
∴△ABC∽△DBA，
∴
=，则
=，解得：AB=6．故选B．
点评：本题利用了弦切角定理，从而得到三角形相似，根据相似三角形的对应边的比相等就可以求出线段的长．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=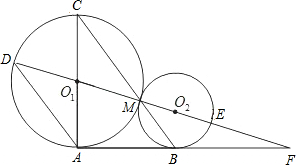
已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
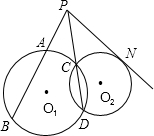如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=
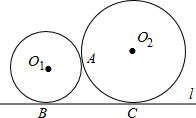已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
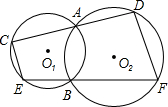已知如图：⊙O1与⊙O2相交于AB两点，过点A、B的直线分别与⊙O1交于C、E，与⊙O2交于D、F，连接CE、DF．