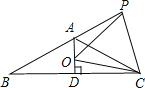
��Ŀ����
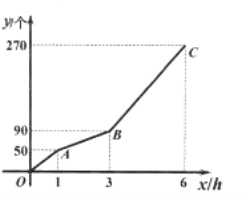
����Ŀ����ֱ�����ǰ�ABC����ͼ1���ã�ֱ�Ƕ���C������ԭ���غϣ�ֱ�DZ�AC��BC�ֱ���x���y���غϣ����С�ABC��30�����������ǰ���y������ƽ�ƣ�����Bƽ�Ƶ�ԭ��Oʱ�˶�ֹͣ����ƽ�Ƶľ���Ϊm��ƽ�ƹ��������ǰ����ڵ�һ�����ֵ����Ϊs��s����m�ĺ���ͼ����ͼ2��ʾ����m���ཻ�ڵ�P��![]() ��0������s���ཻ�ڵ�Q��
��0������s���ཻ�ڵ�Q��
��1����ȷ�����ǰ�ABC�������
��2����ƽ��ǰAB������ֱ�ߵĽ���ʽ��
��3����s����m�ĺ�����ϵʽ����д��Q������꣮
���𰸡���1��S��![]() ����2��y����
����2��y����![]() x+
x+![]() ����3��s��
����3��s��![]() ��m+
��m+![]() ����0��m��
����0��m��![]() ����Q��0��
����Q��0��![]() ����
����
��������
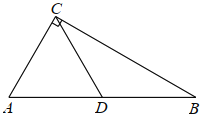
��1�����ݵ�P����ɵ�OB�ij������ݺ�30���ǵ�ֱ�������ε����ʼ����ɶ��������OA�ij������������ABC�������
��2����AB�Ľ���ʽy��kx+b����A��1��0����B��0��![]() �������з����鼴�����b��k��ֵ�������ɵ�ֱ��AB����ʽ��
�������з����鼴�����b��k��ֵ�������ɵ�ֱ��AB����ʽ��
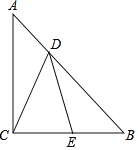
��3�����ƶ������У�AB��x��Ľ���ΪD���ɵ�OB=![]() -m�����ݺ�30���ǵ�ֱ�������ε����ʿ���m��ʾ��OD�ij������ɵó�s����m�Ĺ�ϵʽ����m=0���뼴�������Q���꣮
-m�����ݺ�30���ǵ�ֱ�������ε����ʿ���m��ʾ��OD�ij������ɵó�s����m�Ĺ�ϵʽ����m=0���뼴�������Q���꣮
����m���ཻ�ڵ�P��![]() ��0����
��0����
��m=![]() ʱ��s=0��
ʱ��s=0��
��OB��![]() ��
��
�ߡ�ABC��30����
��AB=2OA��
��OA2+OB2=AB2����OA2+3=4OA2��
��ã�OA=1������ֵ��ȥ��
��S��ABC��![]() ��
��![]() ��
��
��2����B��0��![]() ����A��1��0����
����A��1��0����
��AB�Ľ���ʽy��kx+b��
�� ��
��
�� ��
��
��y����![]() x+
x+![]() ��
��
��3�����ƶ������У�AB��x��Ľ���ΪD��
��OB=![]() ��ƽ�Ƶľ���Ϊm��
��ƽ�Ƶľ���Ϊm��
��ƽ�ƺ�OB��![]() ��m��
��m��
�ߡ�ABC=30����
��BD=2OD��
��OD2+OB2=BD2����OD2+��![]() ��m��2=4OD2
��m��2=4OD2
��OD��1��![]() m��
m��
��s�ڵ�һ���ޣ�OB=![]() ��
��
��0��m��![]() ��
��
��s��![]() ����
����![]() ��m������1��
��m������1��![]() m����
m����![]() ��m+
��m+![]() ��0��m��
��0��m��![]() ����
����
��m��0ʱ��s��![]() ��
��
��Q��0��![]() ����
����

 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�