题目内容
 已知凸四边形ABCD的对角线AC,BD相交于点O,且△ABC,△ACD,△ABD的面积分别为S1=5,S2=10,S3=6.求△ABO的面积(如图).
已知凸四边形ABCD的对角线AC,BD相交于点O,且△ABC,△ACD,△ABD的面积分别为S1=5,S2=10,S3=6.求△ABO的面积(如图).
分析:过B,D分别作AC的垂线,垂足为E,F于是Rt△BEO∽Rt△DFO,设S△AOB=S,则
=
=
,根据S3即可求得S的值,即可解题.
| S |
| S3 |
| BO |
| BD |
| 1 |
| 3 |
解答: 解:过B,D分别作AC的垂线,垂足为E,F.于是
解:过B,D分别作AC的垂线,垂足为E,F.于是
Rt△BEO∽Rt△DFO,所以
=
.
∴
=
=
=
,
由题设
=
=
=
,
=
,
设S△AOB=S,则
=
=
,
所以S=
S3=2.
 解:过B,D分别作AC的垂线,垂足为E,F.于是
解:过B,D分别作AC的垂线,垂足为E,F.于是Rt△BEO∽Rt△DFO,所以
| BE |
| DF |
| BO |
| DO |
∴
| S△ABC |
| S△ADC |
| ||
|
| BE |
| DF |
| BO |
| DO |
由题设
| BO |
| DO |
| S△ABC |
| S△ACD |
| 5 |
| 10 |
| 1 |
| 2 |
| BO |
| BD |
| 1 |
| 3 |
设S△AOB=S,则
| S |
| S3 |
| BO |
| BD |
| 1 |
| 3 |
所以S=
| 1 |
| 3 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比值相等的性质,本题中求证
=
=
是解题的关键.
| S |
| S3 |
| BO |
| BD |
| 1 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
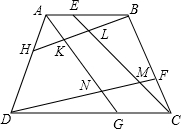 如图,已知凸四边形ABCD,E,F,G,H分别在AB,BC,CD,DA上,且BE=2AE,BF=2CF,DH=2AH,DG=2CG,求证:SKLMN=S△AKH+S△BEL+S△CFM+S△DNG.
如图,已知凸四边形ABCD,E,F,G,H分别在AB,BC,CD,DA上,且BE=2AE,BF=2CF,DH=2AH,DG=2CG,求证:SKLMN=S△AKH+S△BEL+S△CFM+S△DNG. 四块,然后再拼成一个平行四边形?
四块,然后再拼成一个平行四边形?