题目内容
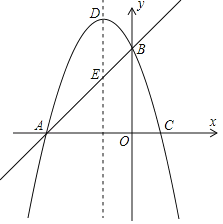
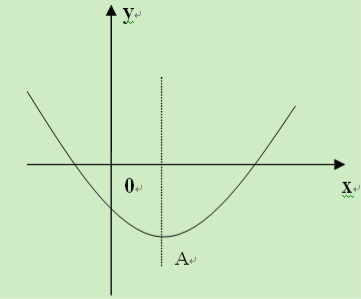
【题目】已知抛物线C1：y=﹣x2+4x﹣3，把抛物线C1先向右平移3个单位长度，再向上平移3个单位长度，得到抛物线C2 ，将抛物线C1和抛物线C2这两个图象在x轴及其上方的部分记作图象M．若直线y=kx+ 
与图象M至少有2个不同的交点，则k的取值范围是________．
【答案】0≤k＜ 
【解析】
首先配方得出二次函数顶点式，求得抛物线C1的顶点坐标，进而利用二次函数平移规律得出抛物线C2，求得顶点坐标，把两点顶点坐标代入即可求得．
y=﹣x2+4x﹣3=
+1，
∴抛物线C1的顶点(2,1)
则将抛物线y=﹣x2+4x﹣3先向右平移3个单位长度，再向上平移3个单位长度，
得到的新的抛物线C2的解析式为：y=
+4.
∴抛物线C2顶点(5,4)，
把(2,1)代入y=kx+ 
(k0)得,1=2k+，
解得k=
，
把(5,4)代入y=kx+ (k0)得,4=5k+ ，
解得k= ，
∴直线y=kx+ (k0)与图象M至少有2个不同的交点,则k的取值范围是0k<.
故答案为：0k<.
练习册系列答案
阅读快车系列答案
相关题目
