题目内容
 如图,已知MA⊥OA于点A,MB⊥OB于点B,AM=BM,连接AB,若∠MAB=20°,则∠AOM的度数位________.
如图,已知MA⊥OA于点A,MB⊥OB于点B,AM=BM,连接AB,若∠MAB=20°,则∠AOM的度数位________.
20°
分析:由MA⊥OA于点A,MB⊥OB于点B,AM=BM,根据角平分线的判定得到OM平分∠AOB,即∠AOM=∠BOM,则∠AMO=∠BMO,即OM平分∠AMB,根据等腰三角形三线合一得到
OM⊥AB,然后利用等角的余角相等得到∠MAB=∠AOM=20°.
解答:∵MA⊥OA于点A,MB⊥OB于点B,AM=BM,
∴OM平分∠AOB,即∠AOM=∠BOM,
∴∠AMO=∠BMO,即OM平分∠AMB,
而AM=BM,
∴OM⊥AB,
∵∠MAB=20°,
∴∠MAB=∠AOM=20°.
故答案为20°.
点评:本题考查了角平分线的判定与性质:角平分线上的点到角的两边的距离相等;到角的两边距离相等的点在这个角的角平分线上.
分析:由MA⊥OA于点A,MB⊥OB于点B,AM=BM,根据角平分线的判定得到OM平分∠AOB,即∠AOM=∠BOM,则∠AMO=∠BMO,即OM平分∠AMB,根据等腰三角形三线合一得到
OM⊥AB,然后利用等角的余角相等得到∠MAB=∠AOM=20°.
解答:∵MA⊥OA于点A,MB⊥OB于点B,AM=BM,
∴OM平分∠AOB,即∠AOM=∠BOM,
∴∠AMO=∠BMO,即OM平分∠AMB,
而AM=BM,
∴OM⊥AB,
∵∠MAB=20°,
∴∠MAB=∠AOM=20°.
故答案为20°.
点评:本题考查了角平分线的判定与性质:角平分线上的点到角的两边的距离相等;到角的两边距离相等的点在这个角的角平分线上.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
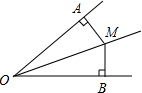 如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( )
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( )| A、50° | B、40° | C、30° | D、20° |
 如图,已知MA⊥OA于点A,MB⊥OB于点B,AM=BM,连接AB,若∠MAB=20°,则∠AOM的度数位
如图,已知MA⊥OA于点A,MB⊥OB于点B,AM=BM,连接AB,若∠MAB=20°,则∠AOM的度数位
