Question

【题目】如图，已知△CAD与△CEB都是等边三角形，BD、EA的延长线相交于点F．

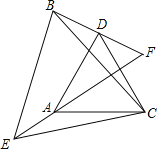
（1）求证：△ACE≌△DCB．

（2）求∠F的度数．

（3）若AD⊥BD，请直接写出线段EF与线段BD、DF之间的数量关系．

Answer 1

【答案】（1）见解析；（2）60°；（3）EF＝BD+2DF.

【解析】

（1）根据等边三角形的性质得到CB=CE，CD=CA，∠BCE=∠DCA=60°，由全等三角形的判定定理即可得到结论；
（2）设BC与EF相交于G，根据全等三角形的性质得到∠1=∠2，根据三角形的内角和即可得到结论；
（3）根据垂直的定义得到∠ADF=90°，求得∠DAF=30°，根据直角三角形的性质得到AF=2DF，根据全等三角形的性质得到AE=BD，于是得到结论．

（1）∵△CAD与△CEB都是等边三角形，

∴CB＝CE，CD＝CA，∠BCE＝∠DCA＝60°，

∴∠BCD＝∠ECA，

∴△ACE≌△DCB（SAS）；

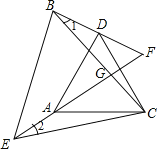
（2）设BC与EF相交于G，

由（1）可知△ACE≌△DCB，

∴∠1＝∠2，

∵∠1+∠BGF+∠F＝∠2+∠AGC+∠BCE＝180°，

而∠BGF＝∠AGC，

∴∠F＝∠BCE＝60°；

（3）EF＝BD+2DF，理由如下：

∵AD⊥BD，

∴∠ADF＝90°，

∵∠F＝60°，

∴∠DAF＝30°，

∴AF＝2DF，

∵△ACE≌△DCB，

∴AE＝BD，

∴EF＝AE+AF＝BD+2DF．