题目内容
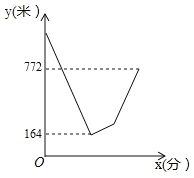
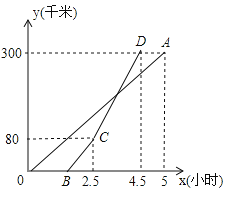
【题目】如图:甲、乙两地相距![]() ,一辆货车和一辆轿车先后从甲地出发驶向乙地,线段
,一辆货车和一辆轿车先后从甲地出发驶向乙地,线段![]() 和折线
和折线![]() 分别表示货车和轿车离甲地的距离
分别表示货车和轿车离甲地的距离![]()
![]() 与货车出发时间
与货车出发时间![]()
![]() 之间的函数关系,请根据图象解答下列问题:
之间的函数关系,请根据图象解答下列问题:
(1)货车的速度为___________![]() ,当轿车到达乙地后,货车距乙地的距离为____________千米;
,当轿车到达乙地后,货车距乙地的距离为____________千米;
(2)求轿车改变速度后![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)轿车到达乙地后,马上沿原路以![]() 段速度返回,求轿车从乙地出发后多长时间再次与货车相遇?
段速度返回,求轿车从乙地出发后多长时间再次与货车相遇?
【答案】(1)60;30;(2)![]() ;(3)
;(3)![]() 小时.
小时.
【解析】
(1)根据函数图象中的数据,可以求得货车的速度和当轿车到达乙地后,货车距乙地的距离;
(2)根据函数图象中的数据可以求得轿车改变速度后y与x的函数关系式;
(3)根据函数图象中的数据可以求得CD段小轿车的速度,从而可以解答本题.
解:(1)由图象可得,
货车的速度为:300÷5=60km/h,
当轿车到达乙地后,货车距乙地的距离为:60×(5-4.5)=30(千米),
故答案为:60,30;
(2)设轿车改变速度后y与x的函数关系式为y=kx+b,![]() ,得
,得![]() ,
,
即轿车改变速度后y与x的函数关系式是y=110x-195(2.5≤x≤4.5);
(3)轿车CD段的速度为:(300-80)÷(4.5-2.5)=110km/h,
设轿车从乙地出发后th时再次与货车相遇,
(110+60)t=300,
解得,t=![]() ,
,
答:轿车从乙地出发后经过![]() 小时再次与货车相遇.
小时再次与货车相遇.

练习册系列答案
相关题目