题目内容
(本小题10分)已知 抛物线
抛物线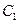 :
: .点F(1,1).
.点F(1,1). (Ⅰ) 求抛物线
(Ⅰ) 求抛物线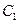 的顶点坐标;
的顶点坐标;
(Ⅱ)
①若抛物线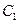 与y轴的交点为A.连接AF,并延长交抛物线
与y轴的交点为A.连接AF,并延长交抛物线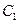 于点B,求证:
于点B,求证:
②抛物线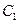 上任意一点P(
上任意一点P(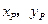 ))(
))( ).连接PF.并延长交抛物线
).连接PF.并延长交抛物线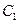 于点Q(
于点Q(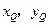 ),试判断
),试判断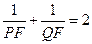 是否成立?请说明理由;
是否成立?请说明理由;
(Ⅲ) 将抛物线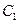 作适当的平移.得抛物线
作适当的平移.得抛物线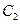 :
: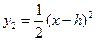 ,若
,若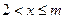 时.
时.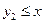

恒成立,求m的最大值.
解 (I)∵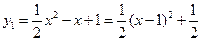 ,
,
∴抛物线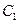 的顶点坐标为(
的顶点坐标为(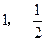 ).
).
(II)①根据题意,可得点A(0,1),
∵F(1,1).
∴AB∥x轴.得AF=BF=1,
②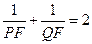 成立.
成立.
理由如下: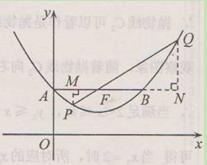
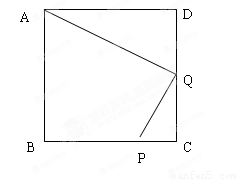
如图,过点P(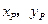 )作PM⊥AB于点M,则FM=
)作PM⊥AB于点M,则FM=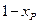 ,PM=
,PM=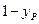 (
( )
)
∴Rt△PMF中,有勾股定理,得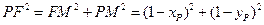
又点P(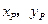 )在抛物线
)在抛物线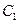 上,
上,
得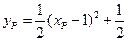 ,即
,即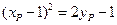
∴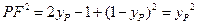
即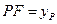 .
.
过点Q(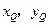 )作QN⊥B,与AB的延长线交于点N,
)作QN⊥B,与AB的延长线交于点N,
同理可得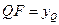 .
.
图文∠PMF=∠QNF =90°,∠MFP=∠NFQ,
=90°,∠MFP=∠NFQ,
∴△PMF∽△QNF
有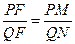
这里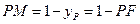 ,
,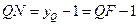
∴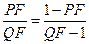
即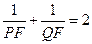
(Ⅲ) 令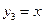 ,
,
设其图象与抛物线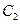 交点的横坐标为
交点的横坐标为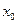 ,
,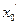 ,且
,且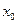 <
<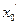 ,
,
∵抛物线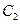 可以看作是抛物线
可以看作是抛物线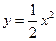 左右平移得到的,
左右平移得到的,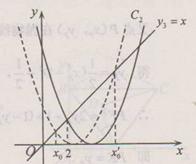
观察图象.随着抛物线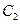 向右不断平移,
向右不断平移,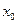 ,
,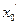 的值不断增大,
的值不断增大,
∴当满足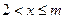 ,.
,.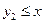 恒成立时,m的最大值在
恒成立时,m的最大值在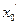 处取得。
处取得。
可得当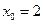 时.所对应的
时.所对应的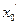 即为m的最大值.
即为m的最大值.
于是,将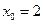 带入
带入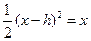 ,
,
有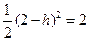
解得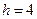 或
或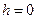 (舍)
(舍)
∴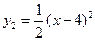
此时,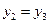 ,得
,得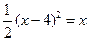
解得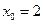 ,
,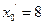
∴m的最大值为8
解析

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目