题目内容
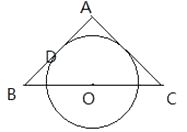
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的任意一动点,点
边上的任意一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,直线
对称,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 边上的高;
边上的高;
(2)当![]() 为何值时,△
为何值时,△![]() 与△
与△![]() 重叠部分的面积最大,并求出最大值;
重叠部分的面积最大,并求出最大值;
(3)连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的度数.
的度数.



【答案】(1)3(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)过点A做AP![]() BC垂足为P,根据题意推出
BC垂足为P,根据题意推出![]() B=
B=![]() C=30
C=30![]() ,再求出AP的值即为BC边上的高;
,再求出AP的值即为BC边上的高;
(2)由对称及AD与DC至少有一段不会超过BC的一半,得出当△ADB![]() 与△ADC完全重合时,即当BD=3
与△ADC完全重合时,即当BD=3![]() 时△ADB
时△ADB![]() 与△ADC重叠部分的面积最大;
与△ADC重叠部分的面积最大;
(3)先判断只有![]() BDB
BDB![]() =90
=90![]() 才符合题意,再分别讨论当点
才符合题意,再分别讨论当点![]() 在点
在点![]() 右侧时或右侧时即可.
右侧时或右侧时即可.
(1)过点![]() 做
做![]() 垂足为
垂足为![]()
∵![]() 且
且![]()
∴![]()
在![]() 中
中![]() ,
,![]()
∴![]()
∴底边![]() 上的高
上的高![]() .
.

(2)当![]() 时,△
时,△![]() 与△
与△![]() 重叠部分的面积最大.
重叠部分的面积最大.
此时![]() 、
、![]() 、
、![]() 三点重合,重叠部分为△
三点重合,重叠部分为△![]() ,其面积为:
,其面积为:
![]()
(理由如下:∵点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,∴△
对称,∴△![]() 与△
与△![]() 关于直线
关于直线![]() 对称,∴△
对称,∴△![]() ≌△
≌△![]() ,∴
,∴![]() ,∵
,∵![]() 与
与![]() 至少有一段不会超过
至少有一段不会超过![]() 的一半,∴
的一半,∴![]() 与
与![]() 至少有一个不会超过
至少有一个不会超过![]() 的一半,∴
的一半,∴![]() 与
与![]() 至少有一个不会超过
至少有一个不会超过![]() 的一半,∴当△
的一半,∴当△![]() 与△
与△![]() 完全重合时,△
完全重合时,△![]() 与△
与△![]() 重叠部分的面积最大,并且最大值为
重叠部分的面积最大,并且最大值为![]() 的一半).
的一半).
(3)由轴对称可知:![]() ,∴
,∴![]()
即当![]() 为直角三角形时,
为直角三角形时,

![]() .
.
如图:当点![]() 在点
在点![]() 右侧时
右侧时
由轴对称可知:![]()
∴.![]()
![]()
![]()
∴![]()
![]()
![]() .
.

如图:当点![]() 在点
在点![]() 左侧时
左侧时
由轴对称可知:![]() .
.
![]()
![]()
∴![]()
![]()
![]()
综上所述,当![]() 为直角三角形时,
为直角三角形时,![]() 的度数为
的度数为![]() 或
或![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目