Question

阅读下列材料：
现给如下定义：以x为自变量的函数用y=f（x）表示，对于自变量x取值范围内的一切值，总有f（-x）=f（x）成立，则称函数y=f（x）为偶函数．用上述定义，我们来证明函数f（x）=x²+1是偶数．
证明：∵f（-x）=（-x）²+1=x²+1=f（x）
∴f（x）是偶函数．
根据以上材料，解答下面的问题：
已知函数
①若f（x）是偶数函数，且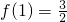，求f（-1）；
②若a=1，求证：f（x）是偶数．

Answer 1

解：①∵f（x）是偶数函数，f（1）=，
∴f（-1）=f（1）=；

②证明：a=1时，f（-x）=-x（+），
=-x（+），
=x（-），
=x（+），
=f（x），
即对于自变量x取值范围内的一切值，总有f（-x）=f（x）成立，
∴f（x）是偶数．
分析：①根据偶函数定义，f（-1）=f（1），进行求解即可；
②把a=1代入，求出f（-x）的表达式，整理后再与f（x）进行比较即可进行判断．
点评：本题考查了偶函数的概念，读懂题目信息，整理出f（-x）的表达式是解题的关键．