题目内容
19.方程组$\left\{\begin{array}{l}{x+y=3}\\{y+z=5}\\{z+x=4}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$.分析 方程组三个方程相加求出x+y+z的值,将每一个方程代入求出x,y,z的值即可.
解答 解:$\left\{\begin{array}{l}{x+y=3①}\\{y+z=5②}\\{z+x=4③}\end{array}\right.$,
①+②+③得:2(x+y+z)=12,即x+y+z=6④,
把①代入④得:z=3,
把②代入④得:x=1,
把③代入④得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
10.若x=2是关于x的一元二次方程x2+x+m=0的一个根,则m是( )
| A. | 6 | B. | 3 | C. | -6 | D. | -3 |
7.下列运算正确的是( )
| A. | x+6x=7x2 | B. | (-4x3)2=16x2 | C. | a8÷a2=a6 | D. | (x-3)2=x2-9 |
 实数a在数轴上的位置如图所示,化简|a-1|+a=1.
实数a在数轴上的位置如图所示,化简|a-1|+a=1.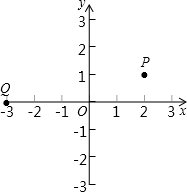 如图,已知Q点的坐标为(-3,0),将点Q向上平移一个单位长度,再向右平移5个单位长度,得到点P.
如图,已知Q点的坐标为(-3,0),将点Q向上平移一个单位长度,再向右平移5个单位长度,得到点P. 的一元二次方程
的一元二次方程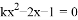 有两个不相等的实数根,则
有两个不相等的实数根,则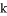 的取值范围是__________.
的取值范围是__________. 的解为( }
的解为( }  B.
B. C.
C. D.
D. 
 _____________.
_____________.