题目内容
 如图:D,E分别是△ABC的边BC,AC上的点,若∠B=∠C,∠ADE=∠AED,∠BAD=30°,则∠EDC=
如图:D,E分别是△ABC的边BC,AC上的点,若∠B=∠C,∠ADE=∠AED,∠BAD=30°,则∠EDC=
- A.30°
- B.25°
- C.15°
- D.10°
C
分析:首先两次运用三角形外角的性质得∠EDC=(∠B+∠BAD-∠EDC)-∠B=30°-∠EDC,然后移项可得结果.
解答:∵∠EDC=∠AED-∠C,∠ADE=∠AED
∴∠EDC=∠ADE-∠B
∵∠ADE=∠B+∠BAD-∠EDC
∴∠EDC=(∠B+∠BAD-∠EDC)-∠B=30°-∠EDC
即2∠EDC=30°,
∴∠EDC=1,5°.
故∠EDC的度数为15°.
故选C.
点评:本题考查了等腰三角形的性质及三角形内角和定理,三角形外角的性质;解决本题的关键是利用外角和相等的角得到所求角和已知角之间的关系.
分析:首先两次运用三角形外角的性质得∠EDC=(∠B+∠BAD-∠EDC)-∠B=30°-∠EDC,然后移项可得结果.
解答:∵∠EDC=∠AED-∠C,∠ADE=∠AED
∴∠EDC=∠ADE-∠B
∵∠ADE=∠B+∠BAD-∠EDC
∴∠EDC=(∠B+∠BAD-∠EDC)-∠B=30°-∠EDC
即2∠EDC=30°,
∴∠EDC=1,5°.
故∠EDC的度数为15°.
故选C.
点评:本题考查了等腰三角形的性质及三角形内角和定理,三角形外角的性质;解决本题的关键是利用外角和相等的角得到所求角和已知角之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

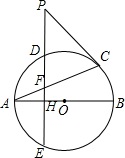 如图:AB、AC分别是⊙O的直径和弦,D为弧AC上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F.P为ED延长线上一点,连PC.
如图:AB、AC分别是⊙O的直径和弦,D为弧AC上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F.P为ED延长线上一点,连PC. 如图,AB和AC分别是⊙O的直径和弦,OD⊥AC于D点,若OA=4,∠A=30°,则BD等于( )
如图,AB和AC分别是⊙O的直径和弦,OD⊥AC于D点,若OA=4,∠A=30°,则BD等于( ) 已知:如图,E、F分别是正方形ABCD边BC、AD上的点,且BE=DF
已知:如图,E、F分别是正方形ABCD边BC、AD上的点,且BE=DF 桌上放着一个圆柱和一个长方体,如图(1),请说出下列三幅图(如图(2))分别是从哪个方向看到的.
桌上放着一个圆柱和一个长方体,如图(1),请说出下列三幅图(如图(2))分别是从哪个方向看到的.