Question

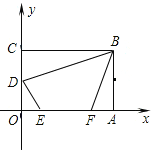
【题目】在平面直角坐标系中，矩形OABC如图所示．点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=3．当四边形BDEF的周长最小时，点E的坐标是（　　）

A. （ ，0） B. （1，0） C. (，0) D. （2，0）

Answer 1

【答案】B

【解析】

以D、E、F为顶点作平行四边形DEF,作出点B关于x轴对称点B',则易得到B'的坐标,D'的坐标,然后利用待定系数法求出直线的解析式,令y=0,确定F点坐标,也即可得到E点坐标.
详解:以D、E、F为顶点作平行四边形DEF,作出点B关于x轴对称点B',如图,

∵B(6,4),
∴ 的坐标为(6,4),
D=EF=3,D(0,2),
∴的坐标为(3,2),
设直线的解析式为y=kx+b,
把(6,-4), (3,2)代入得,
,
解得k=-2,b=8,
∴直线的解析式为y=-2x+8,
令y=0,得-2x+8=0,解得x=4,
∴F(4,0),E(1,0).故选B.