题目内容
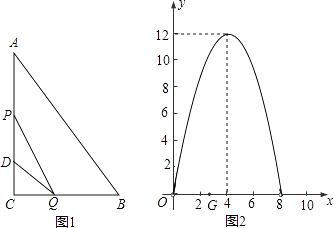
【题目】已知：如图，在平面直角坐标系xOy中，抛物线 
过点A（6，0）和点B（3， 
）．
（1）求抛物线y1的解析式；
（2）将抛物线y1沿x轴翻折得抛物线y2 ， 求抛物线y2的解析式；
（3）在（2）的条件下，抛物线y2上是否存在点M，使△OAM与△AOB相似？如果存在，求出点M的坐标；如果不存在，说明理由．
【答案】
（1）解：依题意，得 
解得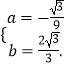 
，
∴抛物线y1的解析式为： 
（2）解：将抛物线y1沿x轴翻折后，仍过点O（0，0），A（6，0），还过点B关于x轴的对称点 
，
设抛物线y2的解析式为： 
，
∴ 
，
解得：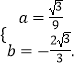 
∴抛物线y2的解析式为 
（3）解：过点B作BC⊥x轴于点C，
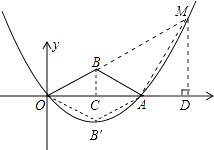
则有 
．
∴∠BOC=30°，∠OBC=60°．
∵OC=3，OA=6，
∴AC=3．
∴∠BAC=30°，∠OBA=120°．
∴OB=AB．
即△OBA是顶角为120°的等腰三角形．
分两种情况：
①当点M在x轴下方时，△OAM就是△OAB'，此时点M的坐标为 
．
②当点M在x轴上方时，假设△OAM∽△OBA，
则有AM=OA=6，∠OAM=120°．
过点M作MD⊥x轴于点D，则∠MAD=60°．
∴ 
，AD=3．∴OD=9．
而（9， 
）满足关系式 ，
即点M在抛物线 上．
根据对称性可知，点 
也满足条件．
综上所述，点M的坐标为 
， 
， 
．
【解析】（1）分别将A、B两点的坐标代入抛物线 y 1 = a x 2 + b x，用待定系数法求解；（2）将抛物线y1沿x轴翻折后，仍过点O，A，还过点B关于x轴的对称点 B '，设抛物线y2的解析式为： y 2 = m x 2 + n x ，用待定系数法即可求解；（3）①当点M在x轴下方时，△OAM就是△OAB，'②当点M在x轴上方时，假设△OAM∽△OBA，分别得出M点的坐标即可。
