题目内容
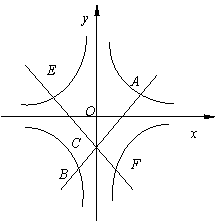
如图,在平面直角坐标系中,双曲线y=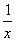 与一次函数y=kx+b (k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线。若新直线与双曲线y=
与一次函数y=kx+b (k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线。若新直线与双曲线y= 相交于点E、F,并使得双曲线y=
相交于点E、F,并使得双曲线y= 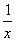 ,y=
,y= ,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则当k为多少时,点A、点E、点B、点F构成的四边形的面积最小。最小值是多少?
,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则当k为多少时,点A、点E、点B、点F构成的四边形的面积最小。最小值是多少?
 |
解:由题得:
 ∵
∵ ∴
∴ 
把点A(1,1)代入y=kx+b中得:1=k+b
∴b=1-k
∴y=kx+(1-k) (2分)
由 得
得

∴

∴点B的坐标为 (2分)
(2分)
由双曲线y=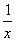 与y=
与y= 与直线y=kx+b以及新直线的对称性可得:
与直线y=kx+b以及新直线的对称性可得:
点A与点E关于y轴对称,点B与点F关于y轴对称,
 ∴E(-1,1)、F
∴E(-1,1)、F
∴AE=2,BF=
AE与BF的距离为k+1
∴梯形

∵k>0
∴当k=1时,梯形 有最小值4
有最小值4

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
保障房建设是民心工程.某市从2008年开始加快保障房建设进程.现统计了该市2008年到2012年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
 |  |
(1)小丽看了统计图后说:“该市2011年新建保障房的套数比2010年少了.”你认为小丽的说法正确吗?请说明理由;
(2)请补全条形统计图;
(3)求这5年平均每年新建保障房的套数.

 ∥
∥ ,
, 且
且 则
则 ( )
( ) 
 的图象,使其与x轴交于两点,且此两点的距离为1个单位,则移动方式可为( )
的图象,使其与x轴交于两点,且此两点的距离为1个单位,则移动方式可为( ) 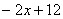 的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.
的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.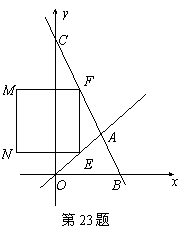 (4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.
(4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.