题目内容
如图平行四边形ABCD的面积为24,E为AB上的中点,连接CE、DE,DE、AC的交点为O,则三角形OCE的面积为( )
A.2
B.3
C.4
D.6
【答案】分析:易得△ECD和△ACD的面积为平行四边形面积的一半;由E为AB上的中点,可得AE:CD=1:2,即可求得AO:CO=1:2,那么S△COD= S△ACD,让△ECD的面积减去△COD面积就是三角形OCE的面积.
S△ACD,让△ECD的面积减去△COD面积就是三角形OCE的面积.
解答:解:∵平行四边形ABCD的面积为24,
∴S△ECD=12,
S△ACD=12,
∵E为AB上的中点,AB=CD,
∴AE:CD=1:2,
∴AO:CO=1:2,
∴S△COD= S△ACD=8,
S△ACD=8,
∴三角形OCE的面积=S△ECD-S△COD=4,故选C.
点评:本题考查了平行四边形的性质,解题的关键是灵活运用同底等高的平行四边形的面积是三角形的面积的2倍;高相等的三角形的面积的比就等于底边的比.
 S△ACD,让△ECD的面积减去△COD面积就是三角形OCE的面积.
S△ACD,让△ECD的面积减去△COD面积就是三角形OCE的面积.解答:解:∵平行四边形ABCD的面积为24,
∴S△ECD=12,
S△ACD=12,
∵E为AB上的中点,AB=CD,
∴AE:CD=1:2,
∴AO:CO=1:2,
∴S△COD=
 S△ACD=8,
S△ACD=8,∴三角形OCE的面积=S△ECD-S△COD=4,故选C.
点评:本题考查了平行四边形的性质,解题的关键是灵活运用同底等高的平行四边形的面积是三角形的面积的2倍;高相等的三角形的面积的比就等于底边的比.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
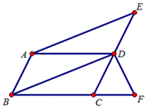 24、如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2
24、如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2 如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
 为点F,DF=2
为点F,DF=2 如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,
如图平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=3,BC=5,∠A=100°,