题目内容
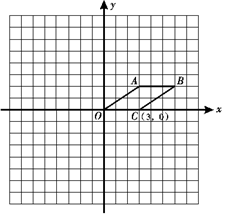
如图,在梯形 中,
中, ∥
∥ ,
, 平分
平分 ,
, 平分线交
平分线交 于
于 ,联结
,联结 .
.

(1)求证:四边形 是菱形;
是菱形;
(2)当 =60°,
=60°, 时,证明:梯形
时,证明:梯形 是等腰梯形.
是等腰梯形.
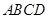 中,
中, ∥
∥ ,
, 平分
平分 ,
, 平分线交
平分线交 于
于 ,联结
,联结 .
.
(1)求证:四边形
 是菱形;
是菱形;(2)当
 =60°,
=60°, 时,证明:梯形
时,证明:梯形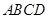 是等腰梯形.
是等腰梯形.证明见解析
(1)∵ ∥
∥ ,∴
,∴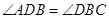 ,
,
又∵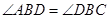 ,∴
,∴ .
.
∴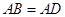 . (2分)
. (2分)
同理有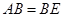 . (1分)
. (1分)
∴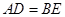 .
.
又∵ ∥
∥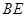 .
.
∴四边形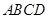 为平行四边形. (2分)
为平行四边形. (2分)
又∵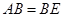 .
.
∴
 为菱形. (1分)
为菱形. (1分)
证明:(2)∵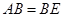 ,
,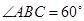 ,
,
∴△ 为等边三角形. (2分)
为等边三角形. (2分)
∴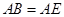 .
.
又∵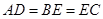 ,
, ∥
∥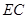 .
.
∴四边形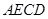 为平行四边形. (2分)
为平行四边形. (2分)
∴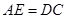 .
.
∴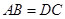 .
.
∴梯形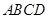 是等腰梯形. (2分)
是等腰梯形. (2分)
(1)根据平行线性质和角平分线定义求出∠ABD=∠ADB,推出AB=AD,AB=BE,推出AD=BE,得出平行四边形ABED,根据菱形的判定推出即可;
(2)推出等边三角形ABE,得出AE=AB,推出平行四边形AECD,推出AE=CD,推出AB=CD即可.
 ∥
∥ ,∴
,∴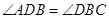 ,
,又∵
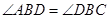 ,∴
,∴ .
.∴
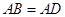 . (2分)
. (2分)同理有
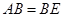 . (1分)
. (1分)∴
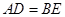 .
.又∵
 ∥
∥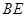 .
.∴四边形
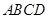 为平行四边形. (2分)
为平行四边形. (2分)又∵
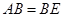 .
.∴
 为菱形. (1分)
为菱形. (1分)证明:(2)∵
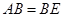 ,
,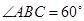 ,
,∴△
 为等边三角形. (2分)
为等边三角形. (2分)∴
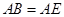 .
.又∵
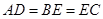 ,
, ∥
∥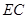 .
.∴四边形
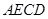 为平行四边形. (2分)
为平行四边形. (2分)∴
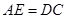 .
.∴
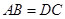 .
.∴梯形
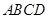 是等腰梯形. (2分)
是等腰梯形. (2分)(1)根据平行线性质和角平分线定义求出∠ABD=∠ADB,推出AB=AD,AB=BE,推出AD=BE,得出平行四边形ABED,根据菱形的判定推出即可;
(2)推出等边三角形ABE,得出AE=AB,推出平行四边形AECD,推出AE=CD,推出AB=CD即可.

练习册系列答案
相关题目
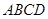 ,有以下四个条件:①
,有以下四个条件:①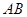 ∥
∥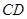 ;②
;②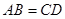 ;③
;③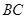 ∥
∥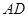 ;④
;④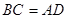 .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形 ACF与
ACF与