题目内容
【题目】正方形ABCD的边长为6cm,点E、M分别是线段BD、AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图1,若点M与点D重合,求证:AF=MN;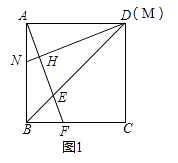
(2)如图2,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以 ![]() cm/s的速度沿BD向点D运动,运动时间为t s.
cm/s的速度沿BD向点D运动,运动时间为t s.
①设BF=y cm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.
【答案】
(1)
解:∵四边形ABCD 是正方形,
∴AD=AB,∠BAD=90°,
∵MN⊥AF,
∴∠AHM=90°,
∴∠BAF+∠MAH=∠MAH+∠AMH=90°,
∴∠BAF=∠AMH,
在△AMN与△ABF中,  ,
,
∴△AMN≌△ABF,
∴AF=MN
(2)
解:①∵AB=AD=6,
∴BD=6 ![]() ,
,
由题意得,DM=t,BE= ![]() t,
t,
∴AM=6﹣t,DE=6 ![]() ﹣
﹣ ![]() t,
t,
∵AD∥BC,
∴△ADE∽△FBE,
∴ ![]() ,即
,即 ![]() ,
,
∴y= ![]() ;
;
②∵BN=2AN,
∴AN=2,BN=4,
由(1)证得∠BAF=∠AMN,∵∠ABF=∠MAN=90°,
∴△ABF∽△AMN,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴BF= ![]() ,
,
由①求得BF= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t=2,
∴BF=3,
∴FN= ![]() =5
=5
【解析】(1)根据四边形的性质得到AD=AB,∠BAD=90°,由垂直的定义得到∠AHM=90°,由余角的性质得到∠BAF=∠AMH,根据全等三角形的性质即可得到结论;(2)①根据勾股定理得到BD=6 ![]() ,由题意得,DM=t,BE=
,由题意得,DM=t,BE= ![]() t,求得AM=6﹣t,DE=6
t,求得AM=6﹣t,DE=6 ![]() ﹣
﹣ ![]() t,根据相似三角形的判定和性质即可得到结论;②根据已知条件得到AN=2,BN=4,根据相似三角形的性质得到BF=
t,根据相似三角形的判定和性质即可得到结论;②根据已知条件得到AN=2,BN=4,根据相似三角形的性质得到BF= ![]() ,由①求得BF=
,由①求得BF= ![]() ,得方程
,得方程 ![]() =
= ![]() ,于是得到结论.
,于是得到结论.
【考点精析】掌握全等三角形的性质和勾股定理的概念是解答本题的根本,需要知道全等三角形的对应边相等; 全等三角形的对应角相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.