题目内容
 (2013•咸宁)如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=
(2013•咸宁)如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=| k | x |
(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
分析:(1)首先求出直线y=2x-2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=OB,AO=AC,即可求出D坐标,由点D在双曲线y=
( x>0)的图象上求出k的值;
(2)首先直线y=2x+b与坐标轴交点的坐标为A(-
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
| k |
| x |
(2)首先直线y=2x+b与坐标轴交点的坐标为A(-
| b |
| 2 |
解答:解:(1)当b=-2时,
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y=
( x>0)的图象上,
∴k=2×2=4.
(2)直线y=2x+b与坐标轴交点的坐标为A(-
,0),B(0,b).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y=
( x>0)的图象上,
∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.
直线OD的解析式为:y=x.
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y=
| k |
| x |
∴k=2×2=4.
(2)直线y=2x+b与坐标轴交点的坐标为A(-
| b |
| 2 |
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y=
| k |
| x |
∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.
直线OD的解析式为:y=x.
点评:本题主要考查反比例函数的综合题的知识点,解答本题的关键是熟练掌握反比例函数的性质以及反比例函数图象的特征,此题难度不大,是一道不错的中考试题.

练习册系列答案
相关题目
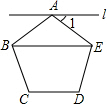 (2013•咸宁)如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为( )
(2013•咸宁)如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为( ) (2013•咸宁)如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
(2013•咸宁)如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( ) (2013•咸宁)如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于
(2013•咸宁)如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 (2013•咸宁)如图,在Rt△AOB中,OA=OB=3
(2013•咸宁)如图,在Rt△AOB中,OA=OB=3