题目内容
【题目】已知:如图,在ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.求ABCD的周长和面积.
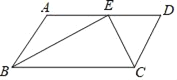
【答案】平行四边形的周长为39cm,面积为60cm2.
【解析】试题分析:根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=13.根据等腰三角形的性质得到AB=CD=![]() AD=
AD=![]() BC=6.5,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
BC=6.5,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
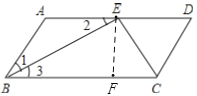
试题解析:∵BE、CE分别平分∠ABC、∠BCD,
∴∠1=∠3=![]() ∠ABC,∠DCE=∠BCE=
∠ABC,∠DCE=∠BCE=![]() ∠BCD,
∠BCD,
∵AD∥BC,AB∥CD,
∴∠2=∠3,∠BCE=∠CED,∠ABC+∠BCD=180°,
∴∠1=∠2,∠DCE=∠CED,∠3+∠BCE=90°,
∴AB=AE,CD=DE,∠BEC=90°,
在直角三角形BCE中,根据勾股定理得:BC=13,
根据平行四边形的对边相等,得到:AB=CD,AD=BC,
∴平行四边形的周长等于:13+13+13=39;
作EF⊥BC于F.根据直角三角形的面积公式得:EF=![]() =
=![]()
所以平行四边形的面积=![]() ×13=60;
×13=60;
即平行四边形的周长为39cm,面积为60cm2.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目