题目内容
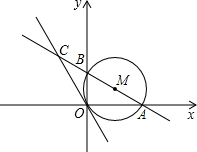已知，如图，半径为1的⊙M经过直角坐标系的原点O，且与x轴、y轴分别交于点A、B，点A的坐标为（| 3 |
分析：在Rt△AOB中，已知了直径AB和OA的长，即可求得∠OAB、∠OBA的度数；而由弦切角定理知∠OAB=∠BOC，进而可由三角形的外角性质求出∠ACO的度数．
解答：解：∵AB=2，OA=
，
∴cos∠BAO=
=
，
∴∠OAB=30°，∠OBA=60°；
∵OC是⊙M的切线，
∴∠BOC=∠BAO=30°，
∴∠ACO=∠OBA-∠BOC=30°．
故答案为：30．
| 3 |
∴cos∠BAO=
| OA |
| AB |
| ||
| 2 |
∴∠OAB=30°，∠OBA=60°；
∵OC是⊙M的切线，
∴∠BOC=∠BAO=30°，
∴∠ACO=∠OBA-∠BOC=30°．
故答案为：30．
点评：此题主要考查了直角三角形的性质、弦切角定理以及三角形的外角性质，难度不大．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
于点A、B，点A的坐标为（
23、已知：如图，⊙O半径为6．过⊙O外一点P作⊙O的切线PA，A为切点，∠OPA=30°．过PO与⊙O的交点B作直线BC交PA于点C，交⊙O于点D．
已知：如图，⊙O半径为5，PC切⊙O于点C，PO交⊙O于点A，PA=4，那么PC的长等于（ ）| A、6 | ||
B、2
| ||
C、2
| ||
D、2
|
，0），⊙M的切线OC与直线AB交于点C．