题目内容
点A（1，2），点B（6，9），点P在y轴上移动，若△PAB的周长取最小值时，点P的坐标是________．
（0，3）
分析：AB的长度一定，要使△PAB的周长取最小值，需要满足PA+PB取最小值，利用轴对称的性质确定点P的位置，求出A'B的函数解析式后即可得出点P的坐标．
解答：
解：过点A作关于y轴的对称点A'，连接A'B，则A'B与y轴的交点即为点P的位置，
∵点A的坐标为（1，2），
∴点A'的坐标为（-1，2），
设直线A'B的解析式为y=kx+b，则
，
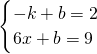解得：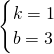
，
即直线A'B的解析式为y=x+3，
令x=0，则y=3．
故点P的坐标为：（0，3）．
故答案为：（0，3）．
点评：本题考查了轴对称求最短路径的问题，解答这类题目可以归结为一个模式：找一个点关于直线的对称点，然后连接对称点与另一个点，则与对称直线的交点即是要求的点．
分析：AB的长度一定，要使△PAB的周长取最小值，需要满足PA+PB取最小值，利用轴对称的性质确定点P的位置，求出A'B的函数解析式后即可得出点P的坐标．
解答：
解：过点A作关于y轴的对称点A'，连接A'B，则A'B与y轴的交点即为点P的位置，∵点A的坐标为（1，2），
∴点A'的坐标为（-1，2），
设直线A'B的解析式为y=kx+b，则
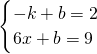，解得：
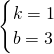，即直线A'B的解析式为y=x+3，
令x=0，则y=3．
故点P的坐标为：（0，3）．
故答案为：（0，3）．
点评：本题考查了轴对称求最短路径的问题，解答这类题目可以归结为一个模式：找一个点关于直线的对称点，然后连接对称点与另一个点，则与对称直线的交点即是要求的点．
练习册系列答案
相关题目
OB，OC的长分别是方程x2-4x+3=0的两根（OB＜OC）．
18、如果将点P绕定点M旋转180°后与点Q重合，那么点P与点Q关于点M对称，定点M叫对称中心，此时，点M是线段PQ的中点．如图，在直角坐标系中，△ABO的顶点A、B、O的坐标分别为（1，0）、（0，1）、（0，0），点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称，点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与点P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称，…，且这些对称中心依次循环，已知P1的坐标是（1，1），点P100的坐标为
（2012•黄浦区二模）已知一次函数y=x+1的图象和二次函数y=x2+bx+c的图象都经过A、B两点，且点A在y轴上，B点的纵坐标为5．
如图，抛物线y1与y2都与x轴交于点O（0，0）和点A，y1的顶点是B（2，-1），y2的顶点是C（2，-3），P是y1上的一个动点，过P作y轴的平行线交y2于点Q，分别过P，Q作x轴的平行线，分别交y1，y2于点P′，Q′，连接P′Q′．
（2013•恩施州）如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．