题目内容
如图，已知在等腰△ABC中，AB=AC=13，BC=10，求底角∠B的三角函数值．分析：过A点作AD⊥BC，将等腰三角形转化为直角三角形，利用勾股定理求AD，利用锐角三角函数的定义求∠B的三角函数值．
解答：
解：过A点作AD⊥BC，垂足为D，
∵AB=AC，∴BD=CD，
在Rt△ABD中，AB=13，BD=5，
由勾股定理，得AD=
=12，
由锐角三角函数的定义，
得sinB=
=
；cosB=
=
；tanB=
=
．
解：过A点作AD⊥BC，垂足为D，∵AB=AC，∴BD=CD，
在Rt△ABD中，AB=13，BD=5，
由勾股定理，得AD=
| 132-52 |
由锐角三角函数的定义，
得sinB=
| AD |
| AB |
| 12 |
| 13 |
| BD |
| AB |
| 5 |
| 13 |
| AD |
| BD |
| 12 |
| 5 |
点评：本题考查了解直角三角形中三角函数的应用，关键是将问题转化到直角三角形中求解，并且要熟练掌握好边角之间的关系．
练习册系列答案
相关题目
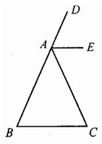21、如图，已知在等腰三角形ABC中，AB=AC，AE∥BC．求证：AE平分∠DAC．
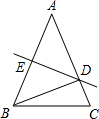如图，已知在等腰△ABC中，如果AB=AC，∠A=40°，DE是AB的垂直平分线，那么∠DBC=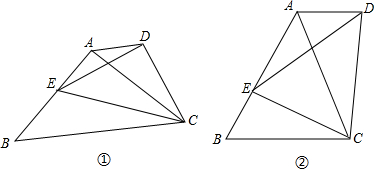
如图，已知在等腰梯形ABCD中，AD∥BC，PA=PD，问PB与PC相等吗？为什么？