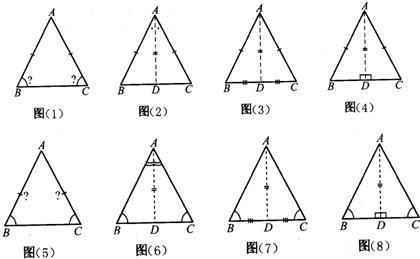
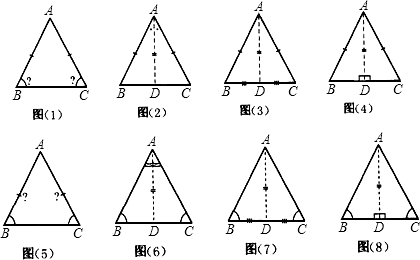
题目内容

已知：

那么

吗？

我是这样想思考的：
∵

（已知）

（）
∴

（）
∴AF∥ED （）
∴

( )
∵

∴

∴AB∥CD ( )
∴

( )
你认为对吗？如果对，请在括号里填写理由。

解析:
略

练习册系列答案

易百分初中同步训练方案系列答案

百分导学系列答案

金钥匙冲刺名校大试卷系列答案

启东黄冈大试卷系列答案

尖子生题库系列答案

功到自然成系列答案

零负担作业系列答案

联动课堂课时作业系列答案

整合集训天天练系列答案

课时训练江苏人民出版社系列答案

相关题目

9、妙趣角：辅助线
问题探讨实录片段：
老师：等腰三角形的两个底角一定相等吗？
同学们异口同声：一定相等！
老师：谁能说说理由？[说着，在图（1）上用符号分别表示了已知“等腰”的条件和“底角为何相等”的疑问．]
小明：如图（2），如果作顶角平分线AD，那么可以根据“SAS”知道△ABD≌△ACD，得到∠B=∠C．
小华：如图（3），如果作底边上的中线，那么可以根据“SSS”，知道△ABD≌△ACD，得到∠B=∠C．
小芳：如图（4），如果作底边上的高，那么可以根据“HL”，知道△ABD≌△ACD，得到∠B=∠C．
老师：非常好！小明、小华和小芳所作的线段虽然名目各异，但是作用相同──都是通过构造一对全等三角形来说明∠B=∠C，所画的这条线段AD，可以称它为“辅助线”．
小强：“辅助线”，可谓名副其实．
老师：上面大家探讨得到：一个三角形中，如果知道两边相等，那么可得这两边的对角也相等，这可简述为“等边对等角”．
小霞：我想也应该有“等角对等边”[说着，画出了图（5），其中，AB、AC两边上的“”无疑也是在征求说理．]
不一会，争先恐后的几位同学在黑板上画出了如下带有“辅助线”的图形[图（6）、（7）、（8）]：

老师期待的目光显然是在说：请你通过观察与思考，对上述3个图形作一评价…

妙趣角：辅助线
问题探讨实录片段：
老师：等腰三角形的两个底角一定相等吗？
同学们异口同声：一定相等！
老师：谁能说说理由？[说着，在图（1）上用符号分别表示了已知“等腰”的条件和“底角为何相等”的疑问．]
小明：如图（2），如果作顶角平分线AD，那么可以根据“SAS”知道△ABD≌△ACD，得到∠B=∠C．
小华：如图（3），如果作底边上的中线，那么可以根据“SSS”，知道△ABD≌△ACD，得到∠B=∠C．
小芳：如图（4），如果作底边上的高，那么可以根据“HL”，知道△ABD≌△ACD，得到∠B=∠C．
老师：非常好！小明、小华和小芳所作的线段虽然名目各异，但是作用相同──都是通过构造一对全等三角形来说明∠B=∠C，所画的这条线段AD，可以称它为“辅助线”．
小强：“辅助线”，可谓名副其实．
老师：上面大家探讨得到：一个三角形中，如果知道两边相等，那么可得这两边的对角也相等，这可简述为“等边对等角”．
小霞：我想也应该有“等角对等边”[说着，画出了图（5），其中，AB、AC两边上的“”无疑也是在征求说理．]
不一会，争先恐后的几位同学在黑板上画出了如下带有“辅助线”的图形[图（6）、（7）、（8）]：

老师期待的目光显然是在说：请你通过观察与思考，对上述3个图形作一评价…

妙趣角：辅助线
问题探讨实录片段：
老师：等腰三角形的两个底角一定相等吗？
同学们异口同声：一定相等！
老师：谁能说说理由？[说着，在图（1）上用符号分别表示了已知“等腰”的条件和“底角为何相等”的疑问．]
小明：如图（2），如果作顶角平分线AD，那么可以根据“SAS”知道△ABD≌△ACD，得到∠B=∠C．
小华：如图（3），如果作底边上的中线，那么可以根据“SSS”，知道△ABD≌△ACD，得到∠B=∠C．
小芳：如图（4），如果作底边上的高，那么可以根据“HL”，知道△ABD≌△ACD，得到∠B=∠C．
老师：非常好！小明、小华和小芳所作的线段虽然名目各异，但是作用相同──都是通过构造一对全等三角形来说明∠B=∠C，所画的这条线段AD，可以称它为“辅助线”．
小强：“辅助线”，可谓名副其实．
老师：上面大家探讨得到：一个三角形中，如果知道两边相等，那么可得这两边的对角也相等，这可简述为“等边对等角”．
小霞：我想也应该有“等角对等边”[说着，画出了图（5），其中，AB、AC两边上的“”无疑也是在征求说理．]
不一会，争先恐后的几位同学在黑板上画出了如下带有“辅助线”的图形[图（6）、（7）、（8）]：

老师期待的目光显然是在说：请你通过观察与思考，对上述3个图形作一评价…