题目内容
定义[a，b，c]为函数y=ax2+bx+c的特征数，下面给出特征数为 [m，1-m，-1]的函数的一些结论：
① 当m＝-1时，函数图象的顶点坐标是（1，0）；
② 当m>0时，函数图象截x轴所得的线段长度大于1；
③ 当m<0时，函数在x>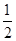
时，y随x的增大而减小；
④ 不论m取何值，函数图象经过一个定点．
其中正确的结论有 （ ）
A．4个 B．3个 C．2个 D．1个
【答案】
B
【解析】
试题分析：①把m=-3代入[2m，1-m，-1-m]，求得[a，b，c]，求得解析式，利用顶点坐标公式解答即可；
②令函数值为0，求得与x轴交点坐标，利用两点间距离公式解决问题；
③首先求得对称轴，利用二次函数的性质解答即可；
④根据特征数的特点，直接得出x的值，进一步验证即可解答．
①当m＝-1时，
，图象的顶点坐标是（1，0），正确；
②令y=0，有
当
时，
，正确；
③当
时，
是一个开口向下的抛物线
其对称轴是
，在对称轴的右边y随x的增大而减小．
因为，
，即对称轴在
的右边，
因此函数在的右边先递增到对称轴位置，再递减，故错误；
④在中，当
时，
所以不论m取何值，函数图象经过一个定点（0，-1），正确
故选B.
考点：二次函数的综合题
点评：此类问题综合性强，难度较大，在中考中比较常见，一般作为压轴题，题目比较典型．
练习册系列答案
相关题目
定义{a，b，c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3}，函数y=-x的“特征数”是{0，-1，0}