��Ŀ����
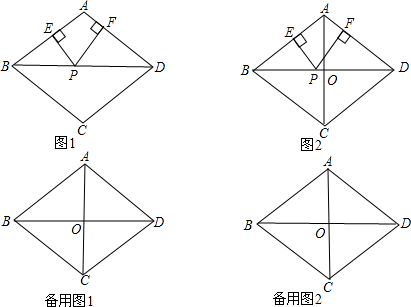
��֪�߳�Ϊ10������ABCD���Խ���BD=16�����߶�BD�ϵ�һ������P������B��D�غϣ��ֱ���AB��AD�����߶Σ�����ֱ�ΪE��F��

��1����ͼ1����֤����PBE�ס�PDE��
��2������PC����PE+PF+PCȡ��Сֵʱ�����߶�BP�ij���
��3����ͼ2���Խ���BD��AC���ڵ�O������POΪ�뾶��PO��0���ġ�P������
�١�P���߶�BC��һ�������㣬�߶�BP���ȵ�ȡֵ��Χ��
�ڡ�P���߶�BC������������ʱ���߶�BP���ȵ�ȡֵ��Χ��

��1����ͼ1����֤����PBE�ס�PDE��
��2������PC����PE+PF+PCȡ��Сֵʱ�����߶�BP�ij���
��3����ͼ2���Խ���BD��AC���ڵ�O������POΪ�뾶��PO��0���ġ�P������
�١�P���߶�BC��һ�������㣬�߶�BP���ȵ�ȡֵ��Χ��
�ڡ�P���߶�BC������������ʱ���߶�BP���ȵ�ȡֵ��Χ��
��������1�������������ʵó���ABD=��ADB���������������ε��ж��Ƴ����ɣ�
��2������AC��BD��O���ӳ�FP��BC��M�����FM�����ó�CPȡ��СֵʱPE+PF+CP��ֵ��С���ó�P��O�غϣ�������ɣ�
��3�����ٹ�P��PG��BC��G����PB=x����P���߶�BO��ʱ��PO=8-x��PG=
x����OP=PBʱ����P����P�㣬8-x=x�����x��ֵ�����ɵó��𰸣��ڸ��ݢٵĽ�����ɵó��𰸣�
��2������AC��BD��O���ӳ�FP��BC��M�����FM�����ó�CPȡ��СֵʱPE+PF+CP��ֵ��С���ó�P��O�غϣ�������ɣ�
��3�����ٹ�P��PG��BC��G����PB=x����P���߶�BO��ʱ��PO=8-x��PG=
| 3 |
| 5 |
����⣺��1�����ı���ABCD�����Σ�
���ABD=��ADB��
��PE��AB��PF��AD��
���BEP=��DFP=90�㣬
���PBE�ס�PDF��
��2����ͼ1������AC��BD��O���ӳ�FP��BC��M��
��FM��BC��
������ABCD��
���ABD=��CBD��
��PM��BC��PE��AB��
��PE=PM��
��PE+PF=PM+PF=FM��
��ֱ��������AOB�У�BO=
BD=8��
��AO=
=
=6��
 ��AC=2AO=12��
��AC=2AO=12��
��S����ABCD=
AC•BD=BC•FM��
��FM=
��
��ˣ�ҪʹPE+PF+PCȡ��Сֵ��ֻҪPCȡ��Сֵ��
���Ե�CP��BDʱ����P��O�غ�ʱ��PC��С����ʱBP=BO=
BD=8��
��3���ٹ�P��PG��BC��G����PB=x����P���߶�BO��ʱ��PO=8-x��PG=
x��
��ͼ2����PO=PGʱ����P��ֱ��BC���У�8-x=
x��x=5��
��ͼ3����OP=PBʱ����P����B�㣬8-x=x��x=4��
 ����0��x��4��x=5ʱ����P���߶�BC��һ�������㣬
����0��x��4��x=5ʱ����P���߶�BC��һ�������㣬
���P���߶�BC��һ�������㣬�߶�BP���ȵ�ȡֵ��Χ��0��BP��4��BP=5ʱ��
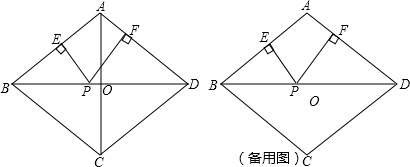
���ɢ�֪����4��x��5ʱ����P���߶�BC�����������㣬
��P���߶�OD��ʱ��PO=x-8��PG=
x��
��PO=PGʱ����P��ֱ��BC���У�x-8=
x��
x=20��BD��
����ʱ��P��������ֱ��BC���У����������ཻ��
�ۺ�������4��BP��5ʱ����P��ֱ��BC�����������㣬
����P���߶�BC������������ʱ���߶�BP���ȵ�ȡֵ��Χ��4��BP��5��
���ABD=��ADB��
��PE��AB��PF��AD��
���BEP=��DFP=90�㣬
���PBE�ס�PDF��
��2����ͼ1������AC��BD��O���ӳ�FP��BC��M��

��FM��BC��
������ABCD��
���ABD=��CBD��
��PM��BC��PE��AB��
��PE=PM��
��PE+PF=PM+PF=FM��
��ֱ��������AOB�У�BO=
| 1 |
| 2 |
��AO=
| AB2-BO2 |
| 102-82 |
 ��AC=2AO=12��
��AC=2AO=12����S����ABCD=
| 1 |
| 2 |
��FM=
| 48 |
| 5 |
��ˣ�ҪʹPE+PF+PCȡ��Сֵ��ֻҪPCȡ��Сֵ��
���Ե�CP��BDʱ����P��O�غ�ʱ��PC��С����ʱBP=BO=
| 1 |
| 2 |
��3���ٹ�P��PG��BC��G����PB=x����P���߶�BO��ʱ��PO=8-x��PG=
| 3 |
| 5 |
��ͼ2����PO=PGʱ����P��ֱ��BC���У�8-x=
| 3 |
| 5 |
��ͼ3����OP=PBʱ����P����B�㣬8-x=x��x=4��
 ����0��x��4��x=5ʱ����P���߶�BC��һ�������㣬
����0��x��4��x=5ʱ����P���߶�BC��һ�������㣬���P���߶�BC��һ�������㣬�߶�BP���ȵ�ȡֵ��Χ��0��BP��4��BP=5ʱ��
���ɢ�֪����4��x��5ʱ����P���߶�BC�����������㣬
��P���߶�OD��ʱ��PO=x-8��PG=
| 3 |
| 5 |
��PO=PGʱ����P��ֱ��BC���У�x-8=
| 3 |
| 5 |
x=20��BD��
����ʱ��P��������ֱ��BC���У����������ཻ��
�ۺ�������4��BP��5ʱ����P��ֱ��BC�����������㣬
����P���߶�BC������������ʱ���߶�BP���ȵ�ȡֵ��Χ��4��BP��5��
���������⿼�������ߵ��ж���ֱ����Բ��λ�ù�ϵ����һԪһ�η��̵�֪ʶ���Ӧ�ã���Ҫ����ѧ���ۺ��������ʽ��������ͼ����������ע�⣺Ҫ���з������۰���

��ϰ��ϵ�д�
�����Ŀ