题目内容
以知∠AOB=150°,OC是∠AOB内的一条射线,射线OD平分∠AOC,射线OE平分∠BOD.
(1)若∠AOD=∠EOC(如图1),求∠AOD的度数.
(2)若∠AOD=a(a≠50°),求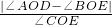 的值.
的值.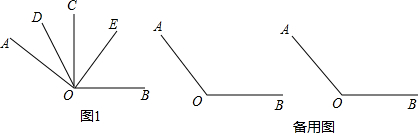
解:(1)设∠AOD=α,
∵∠AOD=∠EOC,
∴∠EOC=α,
∵∠AOB=150°,
∴∠BOD=∠AOB-∠AOD=150°-α,
∵射线OD平分∠AOC,
∴∠DOC=∠AOD=α,
∴BOE=∠AOB-∠AOD-∠DOC-∠EOC=150°-3α,
∵射线OE平分∠BOD,
∴∠BOE= ∠BOD=
∠BOD=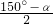 ,
,
∴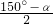 =150°-3α,
=150°-3α,
解得:α=30°,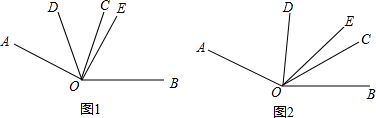
即∠AOD=30°;
(2)当α<50°时,如图1,
∵∠AOD=α,∠BOE= ∠BOD=
∠BOD=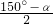 ,
,
∴∠COE=∠BOC-∠BOE=150°-2α-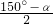 =
=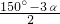 ,
,
∴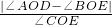 =
=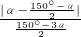 =
=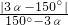 =
=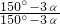 =1;
=1;
当α>50°时,如图2,
∵∠AOD=α,∠BOE= ∠BOD=
∠BOD=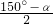 ,
,
∴∠COE=∠BOE-∠BOC=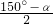 -(150°-2α)=
-(150°-2α)=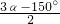 ,
,
∴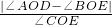 =
=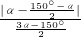 =
=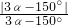 =
=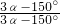 =1.
=1.
分析:(1)首先设∠AOD=α,然后由射线OD平分∠AOC,射线OE平分∠BOD,∠AOD=∠EOC,可求得∠BOE=∠AOB-∠AOD-∠DOC-∠EOC=150°-3α,∠BOE= ∠BOD=
∠BOD=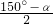 ,则可得方程:
,则可得方程: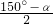 =150°-3α,继而求得答案;
=150°-3α,继而求得答案;
(2)分别从当α<50°与α>50°时去分析求解,即可求得答案.
点评:此题考查了角的有关计算与角平分线的定义.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.
∵∠AOD=∠EOC,
∴∠EOC=α,
∵∠AOB=150°,
∴∠BOD=∠AOB-∠AOD=150°-α,
∵射线OD平分∠AOC,
∴∠DOC=∠AOD=α,
∴BOE=∠AOB-∠AOD-∠DOC-∠EOC=150°-3α,
∵射线OE平分∠BOD,
∴∠BOE=
 ∠BOD=
∠BOD=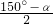 ,
,∴
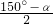 =150°-3α,
=150°-3α,解得:α=30°,

即∠AOD=30°;
(2)当α<50°时,如图1,
∵∠AOD=α,∠BOE=
 ∠BOD=
∠BOD=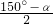 ,
,∴∠COE=∠BOC-∠BOE=150°-2α-
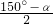 =
=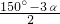 ,
,∴
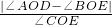 =
=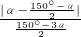 =
=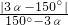 =
=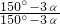 =1;
=1;当α>50°时,如图2,
∵∠AOD=α,∠BOE=
 ∠BOD=
∠BOD=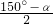 ,
,∴∠COE=∠BOE-∠BOC=
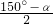 -(150°-2α)=
-(150°-2α)=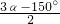 ,
,∴
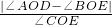 =
=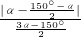 =
=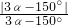 =
=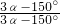 =1.
=1.分析:(1)首先设∠AOD=α,然后由射线OD平分∠AOC,射线OE平分∠BOD,∠AOD=∠EOC,可求得∠BOE=∠AOB-∠AOD-∠DOC-∠EOC=150°-3α,∠BOE=
 ∠BOD=
∠BOD=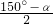 ,则可得方程:
,则可得方程: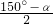 =150°-3α,继而求得答案;
=150°-3α,继而求得答案;(2)分别从当α<50°与α>50°时去分析求解,即可求得答案.
点评:此题考查了角的有关计算与角平分线的定义.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
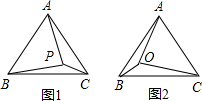 :4.求在以OA、OB、OC为边的三角形中,此三边所对的角度之比.
:4.求在以OA、OB、OC为边的三角形中,此三边所对的角度之比.

