题目内容
如图9(1),在平面直角坐标系中,抛物线![]() 经过A(-1,0)、B(0,3)两点,与x轴交于另一点C,顶点为D.
经过A(-1,0)、B(0,3)两点,与x轴交于另一点C,顶点为D.
(1)求该抛物线的解析式及点C、D的坐标;
(2)经过点B、D两点的直线与x轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
(3)如图9(2)P(2,3)是抛物线上的点,Q是直线AP上方的抛物线上一动点,求△APQ的最大面积和此时Q点的坐标.
 | |||
 | |||
解:(1)∵抛物线![]() 经过A(-1,0)、B(0,3)两点,
经过A(-1,0)、B(0,3)两点,
![]()
![]() ∴
∴![]()
![]() 解得:
解得: ![]()
![]()
![]()
抛物线的解析式为:![]()
∵由![]() ,解得:
,解得:![]()
∴![]()
∵由![]()
![]()
∴D(1,4)
 (2)∵四边形AEBF是平行四边形,
(2)∵四边形AEBF是平行四边形,
∴BF=AE.
设直线BD的解析式为:![]() ,则
,则
∵B(0,3),D(1,4)
![]()
![]() ∴
∴ ![]() 解得:
解得: ![]()
![]()
![]()
∴直线BD的解析式为:![]()
当y=0时,x=-3 ∴E(-3,0), ∴OE=3,
∵A(-1,0)
∴OA=1, ∴AE=2 ∴BF=2,
∴F的横坐标为2, ∴y=3, ∴F(2,3);
(3)如图,设Q![]() ,作PS⊥x轴,QR⊥x轴于点S、R,且P(2,3),
,作PS⊥x轴,QR⊥x轴于点S、R,且P(2,3),
∴AR=![]() +1,QR=
+1,QR=![]() ,PS=3,RS=2-a,AS=3
,PS=3,RS=2-a,AS=3
∴S△PQA=S四边形PSRQ+S△QRA-S△PSA
=![]()
=![]()
 ∴S△PQA=
∴S△PQA=![]()
![]()
![]()
∴当![]() 时,S△PQA的最大面积为
时,S△PQA的最大面积为![]() ,
,
此时Q![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
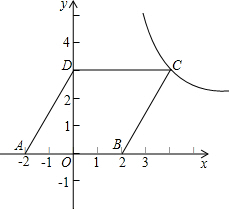 (2013•东城区一模)如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数
(2013•东城区一模)如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数
 如图,已知Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),⊙C的圆心坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交与点E.求:
如图,已知Rt△AOB在平面直角坐标系中,∠AOB=90°,∠BAO=30°,且A的坐标为(3,0),⊙C的圆心坐标为(-1,0),半径为1,若D是⊙C上的一个动点,线段DA与y轴交与点E.求: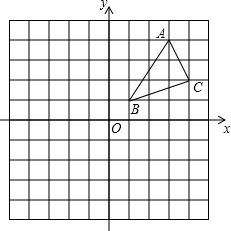 如图,△ABC的顶点都在平面直角坐标系的网格点上.
如图,△ABC的顶点都在平面直角坐标系的网格点上.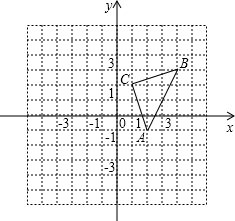 如图,△ABC的顶点都在平面直角坐标系的网格上.
如图,△ABC的顶点都在平面直角坐标系的网格上.