Question

等腰三角形的一个内角为30°，腰长为4，求这个等腰三角形腰上的高．

Answer 1

解：（1）等腰三角形ABC的顶角是30°，BD⊥AC于D，如图所示：
在Rt△ABD中，∵∠A=30°，AB=AC=4，
∴BD=2；

（2）等腰三角形ABC的底角，是30°，BD⊥AC的反向延长线于D，
在Rt△ABD中，∵AB=AC=4，
∴∠C=∠ABC=30°，
∴∠BAD=60°，
∴∠ABD=30°，
∴AD=2．
由勾股定理得BD=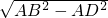==2．
综上所述，这个等腰三角形腰上的高是2或2．
分析：分（1）等腰三角形ABC的顶角是30°；（2）等腰三角形ABC的底角；两种情况讨论即可得到这个等腰三角形腰上的高．
点评：此题主要考查等腰三角形的性质，含30度的直角三角形的性质及勾股定理的综合运用能力．