题目内容
在平面直角坐标系xOy中，已知直线l的参数方程为
（t为参数），以坐标原点为极点，x轴正半轴为极轴，建立极坐标系，曲线C的极坐标方程是
（Ⅰ）写出直线l的普通方程与曲线C的直角坐标方程；
（Ⅱ）设直线l与曲线C相交于A、B两点，求
的值。
解：（I）直线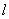
的普通方程为
，
曲线C的直角坐标系方程为
（II）⊙C的圆心（0，0）到直线
的距离
-
∴
∵
故
．
练习册系列答案
阅读快车系列答案
相关题目
与圆心为C的圆
相交于A，B两点，且
，则实数a的值为
或
（B）
（D）某商场销售某种品牌的空调器，每周周初购进一定数量的空调器，商场每销售一台空调器可获利500元，若供大于求，则每台多余的空调器需交保管费100元；若供不应求，则可从其他商店调剂供应，此时每台空调器仅获利润200元。
（Ⅰ）若该商场周初购进20台空调器，求当周的利润（单位：元）关于当周需求量n（单位：台，
）的函数解析式
；
（Ⅱ）该商场记录了去年夏天（共10周）空调器需求量n（单位：台），整理得下表：
| 周需求量n | 18 | 19 | 20 | 21 | 22 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率，若商场周初购进20台空调器，X表示当周的利润（单位：元），求X的分布列及数学期望。
_____ 
（填“>”或“<”或“=”）.
_______；