题目内容
 如图,已知⊙O是△ABC的内切圆,切点为D、E、F,
如图,已知⊙O是△ABC的内切圆,切点为D、E、F,
(1)若∠A=x,∠EDF=y,求y与x的函数关系式.
(2)若∠A=90°,AB=8,BC=10,求⊙O的半径.
 解:(1)连接OE、OF.
解:(1)连接OE、OF.∵⊙O是△ABC的内切圆,切点为D、E、F,
∴∠EOF=2y,∠OEA=∠OFA=90°,
∴∠A+∠EOF=360°-90°-90°=180°,
∴y=90°-
 x,
x,答:y与x的函数关系式是y=90°-
 x.
x.(2)设圆O的半径是r.
由勾股定理得:AC=
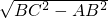 =6,
=6,∵⊙O是△ABC的内切圆,切点为D、E、F,
∴AE=AF,CD=CF,BE=BD,∠OEA=∠OFA=∠A=90°,OE=OF,
∴四边形OEAF是正方形,
∴OE=OF=AE=AF=r,
∴AC-r+AB-r=BC,
∴6-r+8-r=10,
∴r=2.
答:⊙O的半径是2.
分析:(1)连接OE、OF,求出∠EOF=2y,∠OEA=∠OFA=90°,根据四边形的内角和定理求出即可;
(2)根据勾股定理求出AC,推出AE=AF,CD=CF,BE=BD,∠OEA=∠OFA=∠A=90°,OE=OF,证四边形OEAF是正方形,根据AC-r+AB-r=BC代入求出即可.
点评:本题主要考查对正方形的性质和判定,切线长定理,圆周角定理,勾股定理,四边形的内角和定理,三角形的内切圆与内心等知识点的理解和掌握,能熟练地运用性质进行推理是解此题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
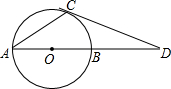 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD= 如图,已知A是半径为1的⊙O上一点,以A为圆心,AO为半径画弧交⊙O于点B、C;以C为圆心,CO为半径画弧交⊙O于点D、A.则图中阴影面积为
如图,已知A是半径为1的⊙O上一点,以A为圆心,AO为半径画弧交⊙O于点B、C;以C为圆心,CO为半径画弧交⊙O于点D、A.则图中阴影面积为 (2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么, (2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.