Question

【题目】如图，已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E，EF⊥AB交AB的延长线于点F，EG⊥AC交于点G．

求证：（1）BF=CG；（2）AF=（AB+AC）．

Answer 1

【答案】（1）见详解；（2）见详解

【解析】

（1）根据线段垂直平分线求出BE=CE，根据角平分线性质求出EF=GE，即可Rt△BFE≌Rt△CGE；
（2）证明△AFE≌△AGE，推出AF=AG，即可得出答案．

证明：（1）连接BE和CE，

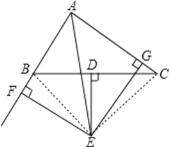
∵DE是BC的垂直平分线，
∴BE=CE，
∵AE平分∠BAC，EF⊥AB，EG⊥AC，
∴∠BFE=∠EGC=90°，EF=EG，
在Rt△BFE和Rt△CGE中

∴Rt△BFE≌Rt△CGE（HL），
∴BF=CG；

（2）∵AE平分∠BAC，EF⊥AB，EG⊥AC，
∴∠AFE=∠AGE=90°，∠FAE=∠GAE，
在△AFE和△AGE中

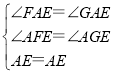
∴△AFE≌△AGE，
∴AF=AG，
∵BF=CG，
∴（AB+AC）=（AF-BF+AG+CG）
=（AF+AF）
=AF，
即AF=（AB+AC）．