题目内容
在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交与点D,E,且∠CBD=∠A.
(1)判断直线BD与⊙O的位置关系,并证明你的结论.
(2)若AD:AO=6:5,BC=3,求BD的长.

考点:
切线的判定.
分析:
(1)连接OD,DE,求出∠ADE=90°=∠C推出DE∥BC∴∠EDB=∠CBD=∠A,根据∠A+∠OED=90°求出∠![]() EDB+∠ODE=90
EDB+∠ODE=90![]() °,根据切线的判定推出即可;
°,根据切线的判定推出即可;
(2)求出AD:DE:AE=6:8:10,求出△ADE∽△ACB,推出DC:BC:BD=AD:DE:AE=6:8:10,代入求出即可.
解答:
(1)直线BD与⊙O的位置关系是相切,
证明:连接OD,DE,
∵∠C=90°,
∴∠CBD+∠CDB=90°,
∵∠A=∠CBD,
∴∠A+∠CDB=90°,
∵OD=OA,
∴∠A=∠ADO,
∴∠ADO+∠CDB=90°,
∴∠ODB=180°﹣90°![]() =90°,
=90°,
∴OD⊥BD,
∵OD为半径,
∴BD是⊙O切线;
(2)解:∵AD:AO=6:5,
∴![]() =
=![]() ,
,
∴由勾股定理得:AD:DE:AE=6:8:10,
∵AE是直径,
∴∠ADE=∠C=90°,
∵∠CBD=∠A,
∴△ADE∽△ACB,
∴DC:BC:BD=AD:DE:AE=6:8:10,
∵BC=3,
∴BD=![]() .
.

点评:
本题考查了切线的判定,平行线性质和判定,等腰三角形性质和判定,相似三角形的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
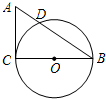 在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D. (2013•湖州)如图,已知在Rt△ACB中,∠C=90°,AB=13,AC=12,则cosB的值为
(2013•湖州)如图,已知在Rt△ACB中,∠C=90°,AB=13,AC=12,则cosB的值为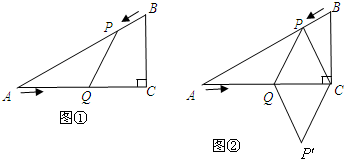
 (2013•丹东一模)在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
(2013•丹东一模)在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )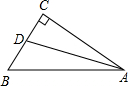 如图所示,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=16,BD=10,则点D到AB的距离是( )
如图所示,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=16,BD=10,则点D到AB的距离是( )