题目内容
已知AB是⊙O的直径,弦CD⊥AB,垂足为H,AH=5,CD= ,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y.
,点E在⊙O上,射线AE与射线CD相交于点F,设AE=x,DF=y.(1)求⊙O的半径;
(2)如图,当点E在弧AD上时,求y与x之间的函数解析式,并写出函数的定义域;
(3)如果EF=
 ,求DF的长.
,求DF的长.
【答案】分析:(1)连接OD,设⊙O的半径OA=OD=r,根据垂径定理得DH= DC=2
DC=2 ,在Rt△OHD中利用勾股定理得到r2-(5-r)2=(2
,在Rt△OHD中利用勾股定理得到r2-(5-r)2=(2 )2,然后解方程即可得到圆的半径;
)2,然后解方程即可得到圆的半径;
(2)作OG⊥AE,垂足为G,根据垂径定理得AG= AE=
AE= x且易得△AOG∽△AFH,则AG:AH=AO:AF,可解得AF=
x且易得△AOG∽△AFH,则AG:AH=AO:AF,可解得AF= ,再在Rt△AHF中利用勾股定理得到FH=
,再在Rt△AHF中利用勾股定理得到FH= =
=
 ,然后利用DF=FH-DH即可得到y与x的关系式,当E与D重合时,x最大,则有0<x≤3
,然后利用DF=FH-DH即可得到y与x的关系式,当E与D重合时,x最大,则有0<x≤3 ;
;
(3)分类讨论:当点E在弧AD上时,由AF-AE=EF可解出x=6,再代入y与x的关系式中得到DF= ;当点E在弧DB上时,由AE-AF=EF,可求得x=
;当点E在弧DB上时,由AE-AF=EF,可求得x= ,然后根据勾股定理计算出BE=
,然后根据勾股定理计算出BE= ,再利用△AHF∽△AEB得到FH:BE=AH:AE,解得FH=
,再利用△AHF∽△AEB得到FH:BE=AH:AE,解得FH= ,所以DF=DH-FH=2
,所以DF=DH-FH=2 -
- ;当点E在BC弧上时,同上得FH=
;当点E在BC弧上时,同上得FH= ,然后利用DF=DH+FH计算即可.
,然后利用DF=DH+FH计算即可.
解答: 解:(1)连接OD,设⊙O的半径OA=OD=r,
解:(1)连接OD,设⊙O的半径OA=OD=r,
∵AB是⊙O的直径,弦CD⊥AB,
∴DH= DC=
DC= ×4
×4 =2
=2 ,
,
在Rt△OHD中,∵OD2-OH2=DH2,OH2=(AH-OA)2=(5-r)2,
∴r2-(5-r)2=(2 )2,解得r=
)2,解得r= ,
,
∴⊙O的半径为 ;
;
(2)作OG⊥AE,垂足为G,如图,
∴AG= AE=
AE= x,
x,
∴△AOG∽△AFH,
∴AG:AH=AO:AF,即 x:5=
x:5= :AF,解得AF=
:AF,解得AF= ,
,
∴FH= =
= =
=
 ,
,
∵DF=FH-DH,
∴y关于x的函数解析式为y=
 -2
-2 ,
,
定义域为0<x≤3 ;
;
(3)当点E在弧AD上时,如图,∵AF-AE=EF,即 -x=
-x= ,
,
化为整式方程得2x2+3x-90=0,解得x1=- (舍去),x2=6,
(舍去),x2=6,
∴DF=y=
 -2
-2 =
= ;
;
当点E在弧DB上时,如图,∵AE-AF=EF,即x- =
= ,
,
化为整式方程得2x2-3x-90=0,解得x1= ,x2=6(舍去),
,x2=6(舍去),
∵AB为直径,
∴∠E=90°,
∴△AHF∽△AEB,BE= =
= ,
,
∴FH:BE=AH:AE,即FH: =5:
=5: ,解得FH=
,解得FH=
∴DF=DH-FH=2 -
-
当点E在BC弧上时,同上得FH= ,
,
∴DF=DH+FH=2 +
+ .
.
点评:本题考查了圆的综合题:垂径定理和圆周角定理在有关圆的几何证明或几何计算中常用到;利用三角形相似比或勾股定理进行计算几何是常用的方法.
 DC=2
DC=2 ,在Rt△OHD中利用勾股定理得到r2-(5-r)2=(2
,在Rt△OHD中利用勾股定理得到r2-(5-r)2=(2 )2,然后解方程即可得到圆的半径;
)2,然后解方程即可得到圆的半径;(2)作OG⊥AE,垂足为G,根据垂径定理得AG=
 AE=
AE= x且易得△AOG∽△AFH,则AG:AH=AO:AF,可解得AF=
x且易得△AOG∽△AFH,则AG:AH=AO:AF,可解得AF= ,再在Rt△AHF中利用勾股定理得到FH=
,再在Rt△AHF中利用勾股定理得到FH= =
=
 ,然后利用DF=FH-DH即可得到y与x的关系式,当E与D重合时,x最大,则有0<x≤3
,然后利用DF=FH-DH即可得到y与x的关系式,当E与D重合时,x最大,则有0<x≤3 ;
;(3)分类讨论:当点E在弧AD上时,由AF-AE=EF可解出x=6,再代入y与x的关系式中得到DF=
 ;当点E在弧DB上时,由AE-AF=EF,可求得x=
;当点E在弧DB上时,由AE-AF=EF,可求得x= ,然后根据勾股定理计算出BE=
,然后根据勾股定理计算出BE= ,再利用△AHF∽△AEB得到FH:BE=AH:AE,解得FH=
,再利用△AHF∽△AEB得到FH:BE=AH:AE,解得FH= ,所以DF=DH-FH=2
,所以DF=DH-FH=2 -
- ;当点E在BC弧上时,同上得FH=
;当点E在BC弧上时,同上得FH= ,然后利用DF=DH+FH计算即可.
,然后利用DF=DH+FH计算即可.解答:
 解:(1)连接OD,设⊙O的半径OA=OD=r,
解:(1)连接OD,设⊙O的半径OA=OD=r,∵AB是⊙O的直径,弦CD⊥AB,
∴DH=
 DC=
DC= ×4
×4 =2
=2 ,
,在Rt△OHD中,∵OD2-OH2=DH2,OH2=(AH-OA)2=(5-r)2,
∴r2-(5-r)2=(2
 )2,解得r=
)2,解得r= ,
,∴⊙O的半径为
 ;
;(2)作OG⊥AE,垂足为G,如图,
∴AG=
 AE=
AE= x,
x,
∴△AOG∽△AFH,
∴AG:AH=AO:AF,即
 x:5=
x:5= :AF,解得AF=
:AF,解得AF= ,
,∴FH=
 =
= =
=
 ,
,∵DF=FH-DH,
∴y关于x的函数解析式为y=

 -2
-2 ,
,定义域为0<x≤3
 ;
;(3)当点E在弧AD上时,如图,∵AF-AE=EF,即
 -x=
-x= ,
,
化为整式方程得2x2+3x-90=0,解得x1=-
 (舍去),x2=6,
(舍去),x2=6,∴DF=y=

 -2
-2 =
= ;
;当点E在弧DB上时,如图,∵AE-AF=EF,即x-
 =
= ,
,化为整式方程得2x2-3x-90=0,解得x1=
 ,x2=6(舍去),
,x2=6(舍去),∵AB为直径,
∴∠E=90°,
∴△AHF∽△AEB,BE=
 =
= ,
,∴FH:BE=AH:AE,即FH:
 =5:
=5: ,解得FH=
,解得FH=
∴DF=DH-FH=2
 -
-
当点E在BC弧上时,同上得FH=
 ,
,∴DF=DH+FH=2
 +
+ .
.点评:本题考查了圆的综合题:垂径定理和圆周角定理在有关圆的几何证明或几何计算中常用到;利用三角形相似比或勾股定理进行计算几何是常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
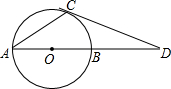 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=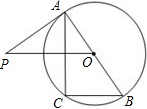 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.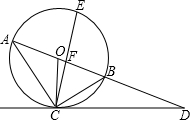

 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A,