题目内容
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值5.
时,函数有最大值5.
(1)求此二次函数图象与坐标轴的交点;
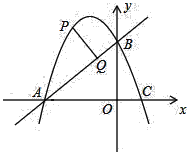
(2)将函数![]() 图象x轴下方部分沿x轴向上翻折,得到的新图象与直线
图象x轴下方部分沿x轴向上翻折,得到的新图象与直线![]() 恒有四个交点,从左到右,四个交点依次记为
恒有四个交点,从左到右,四个交点依次记为![]() ,当以
,当以![]() 为直径的圆与
为直径的圆与![]() 轴相切时,求
轴相切时,求![]() 的值.
的值.
(3)若点![]() 是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程
是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程![]() 恒有实数根时,求实数k的最大值.
恒有实数根时,求实数k的最大值.
【答案】(1) 抛物线与![]() 轴交于
轴交于![]() ;(2)
;(2)![]() ;(3)实数k的最大值为3.
;(3)实数k的最大值为3.
【解析】分析:(1)求出对称轴x=1,结合a>0,可知当![]() 时,
时,![]() 随
随![]() 增大而增大,所以x=4时,y=5,把以x=4时,y=5代入解析式求出a的值,然后解方程
增大而增大,所以x=4时,y=5,把以x=4时,y=5代入解析式求出a的值,然后解方程![]() 即可;
即可;
(2)由折叠部分对应的解析式:![]() ,可知
,可知![]() ,解方程
,解方程![]() ,求出B、C的坐标,然后根据
,求出B、C的坐标,然后根据![]() 列方程即可求出n的值;
列方程即可求出n的值;
(3)根据△≥0求出k的取值范围,即![]() ,再结合
,再结合![]() ,即可求得实数k的最大值.
,即可求得实数k的最大值.
详解:(1) 抛物线![]() 的对称轴为:
的对称轴为:![]() .
.
![]()
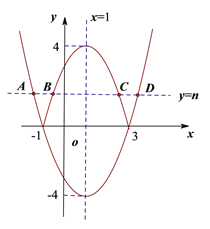
![]() ,抛物线开口向上,大致图象如图所示.
,抛物线开口向上,大致图象如图所示.
![]() 当
当![]() 时,
时,![]() 随
随![]() 增大而增大;
增大而增大;
由已知:当![]() 时,函数有最大值5.
时,函数有最大值5.
![]() 当
当![]() 时,
时, ![]() ,
,
![]() .
.
![]()
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
![]() 抛物线与
抛物线与![]() 轴交于
轴交于![]() ,
,
抛物线与![]() 轴交于
轴交于![]() .
.
(2)![]() ,
,
其折叠得到的部分对应的解析式为:![]() ,其顶点为
,其顶点为![]()
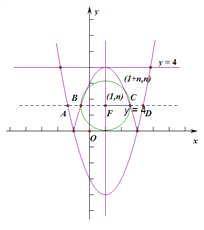
![]() 图象与直线
图象与直线![]() 恒有四个交点,
恒有四个交点,
![]()
![]()
由![]() ,解得
,解得![]() ,
,
![]() ,
,![]() .
.
当以![]() 为直径的圆与
为直径的圆与![]() 轴相切时,
轴相切时,![]() .
.
即:![]() ,
,
![]() ,
,
![]() ,
,
得![]() ,
,![]()
![]() ,
,
![]()
![]() .
.
(另法:∵BC直径,且⊙F与x轴相切,
∴FC=y=n,
∵对称轴为直线x=1,
∴F(1,n),则C(1+n,n),
又∵C在![]() 上,
上,
∴![]() ,
,
得![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
(3)若关于m的一元二次方程![]() 恒有实数根,则须
恒有实数根,则须
![]() 恒成立,
恒成立,
即![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
![]() 点
点![]() 是(2)中翻折得到的抛物线弧部分上任意一点,
是(2)中翻折得到的抛物线弧部分上任意一点,
![]() ,
,
![]()
![]() ,(
,( ![]() 取
取 ![]() 值之下限)
值之下限)
![]() 实数k的最大值为3.
实数k的最大值为3.

【题目】某校为了解同学们课外阅读名著的情况,在八年级随机抽查了20名学生,调查结果如表所示:
课外名著阅读量(本) | 8 | 9 | 10 | 11 | 12 |
学生人数 | 3 | 3 | 4 | 6 | 4 |
关于这20名学生课外阅读名著的情况,下列说法错误的是( )
A.中位数是10B.平均数是10.25C.众数是11D.阅读量不低于10本的同学点70%