题目内容
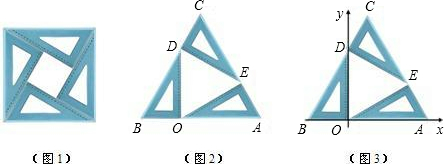
如图1是由四块全等的含有30°角的直角三角板拼成的正方形,已知里面小正方形的边长为 .如图2,取其中的三块直角三角板拼成等边三角形ABC,再以O为原点,AB所在直线为x轴建立平面直角坐标系.
.如图2,取其中的三块直角三角板拼成等边三角形ABC,再以O为原点,AB所在直线为x轴建立平面直角坐标系.
(1)求等边△ABC的面积;
(2)求BC边所在直线的解析式;
(3)将第四块直角三角板与△CDE重合,然后绕点E按逆时针方向旋转60°后得△EC'D',问点C'是否落在直线BC上?请你作出判断,并说明理由.

解:(1)如图,作高CF,
由已知得 ,
,
由正三角形性质得 ,
,
∴ .
.
∴ .
.

(2)由已知:C点坐标是( ,
, ),B点坐标是(-1,0),
),B点坐标是(-1,0),
设直线BC的解析式为y=kx+b,
∴ ,
,
解之 ,
,
∴直线BC的解析式为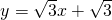 .
.
(3)点C′落在直线BC上.
如图,作C′H⊥AB于H,
由∠C′OB=60°及OC′=1,得,
∴C′的坐标是( ),满足
),满足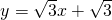
∴点C′落在BD上.
分析:(1)如要求等边△ABC的面积;可作高CF,交AB于F,有题可知AB=3,利用勾股定理可求出CF的值,所以△ABC的面积= AB•CF问题得解;
AB•CF问题得解;
(2)设直线BC的解析式为y=kx+b,由图形可求出B,C点的坐标,把B,C的坐标分别代入,解关于k,b的方程组,可得问题答案;
(3)若要知道点C'是否落在直线BC上,可求出C′点的坐标,代入直线BC的解析式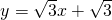 ,等式成立则在,不成立,则不在.
,等式成立则在,不成立,则不在.
点评:本题考查了一次函数与几何图形(等边三角形)问题首先要根据题意画出草图,结合图形分析其中的几何图形,从已知函数图象中获取信息,求出函数值、函数表达式,并解答相应的问题.
由已知得
 ,
,由正三角形性质得
 ,
,∴
 .
.∴
 .
.
(2)由已知:C点坐标是(
 ,
, ),B点坐标是(-1,0),
),B点坐标是(-1,0),设直线BC的解析式为y=kx+b,
∴
 ,
,解之
 ,
,
∴直线BC的解析式为
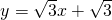 .
.(3)点C′落在直线BC上.
如图,作C′H⊥AB于H,
由∠C′OB=60°及OC′=1,得,
∴C′的坐标是(
 ),满足
),满足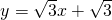
∴点C′落在BD上.
分析:(1)如要求等边△ABC的面积;可作高CF,交AB于F,有题可知AB=3,利用勾股定理可求出CF的值,所以△ABC的面积=
 AB•CF问题得解;
AB•CF问题得解;(2)设直线BC的解析式为y=kx+b,由图形可求出B,C点的坐标,把B,C的坐标分别代入,解关于k,b的方程组,可得问题答案;
(3)若要知道点C'是否落在直线BC上,可求出C′点的坐标,代入直线BC的解析式
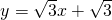 ,等式成立则在,不成立,则不在.
,等式成立则在,不成立,则不在.点评:本题考查了一次函数与几何图形(等边三角形)问题首先要根据题意画出草图,结合图形分析其中的几何图形,从已知函数图象中获取信息,求出函数值、函数表达式,并解答相应的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
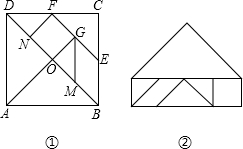 对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
 对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.

