题目内容
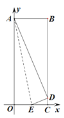
【题目】在平面直角坐标系中，平行四边形
如图放置，点
、
的坐标分别是
、
，将此平行四边形绕点
顺时针旋转
，得到平行四边形
．
如抛物线经过点、、
，求此抛物线的解析式；
在情况下，点
是第一象限内抛物线上的一动点，问：当点在何处时，
的面积最大？最大面积是多少？并求出此时的坐标；
在的情况下，若
为抛物线上一动点，
为
轴上的一动点，点
坐标为
，当、、
、构成以
作为一边的平行四边形时，求点的坐标．
【答案】(1) 抛物线的解析式为：
；(2) 当
时，
的面积最大，最大值
，
的坐标为：
；(3) 点
的坐标为：
，
，
，
【解析】
（1）由平行四边形ABOC绕点O顺时针旋转90°，得到平行四边形A′B′OC′，且点A的坐标是（0，4），可求得点A′的坐标，然后利用待定系数法即可求得经过点C、A、A′的抛物线的解析式；
（2）首先连接AA′，设直线AA′的解析式为：y=kx+b，利用待定系数法即可求得直线AA′的解析式，再设点M的坐标为：（x，-x2+3x+4），继而可得△AMA′的面积，继而求得答案；
（3）分别从BQ为边与BQ为对角线去分析求解即可求得答案．
解：
∵平行四边形
绕点
顺时针旋转
，得到平行四边形
，且点
的坐标是
，
∴点
的坐标为：
，
∵点、
的坐标分别是、
，抛物线经过点、、，
设抛物线的解析式为：
，
∴
，
解得：
，
∴此抛物线的解析式为：；
连接
，设直线的解析式为：
，
∴
，
解得：
，
∴直线的解析式为：
，
设点的坐标为：
，
则
，
∴当时，的面积最大，最大值，
∴的坐标为：；
设点的坐标为，当，
，
，
构成平行四边形时，
∵平行四边形中，点、的坐标分别是、，
∴点的坐标为
，
∵点坐标为
，为抛物线上一动点，为
轴上的一动点，
①当
为边时，
，
，
∵
，
∴
，
当
时，解得：
，
，
∴，；
当
时，解得：
，
，
∴，；
②当为对角线时，
，
，此时与
，
重合；
综上可得：点的坐标为：，，，
名校课堂系列答案
