题目内容
 如图,O为坐标原点,边长为
如图,O为坐标原点,边长为 的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在某抛物线的图象上,则该抛物线的解析式可能为
的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在某抛物线的图象上,则该抛物线的解析式可能为
- A.y=
 x2
x2 - B.y=-
 x2
x2 - C.y=-
 x2
x2 - D.y=-3x2
B
分析:过点B向x轴引垂线,连接OB,可得OB的长度,进而得到点B的坐标,代入二次函数解析式即可求解.
解答:如图,作BE⊥x轴于点E,连接OB,
∵正方形OABC绕顶点O顺时针旋转75°,
∴∠AOE=75°,
∵∠AOB=45°,
∴∠BOE=30°,
∵OA= ,
,
∴OB=2,
∴BE= OB=1,
OB=1,
∴OE=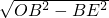 =
= ,
,
∴点B坐标为( ,-1),
,-1),
代入y=ax2(a<0)得a=- ,
,
∴y=- x2x,
x2x,
故选B.
点评:本题考查用待定系数法求函数解析式和勾股定理的运用,解题的关键是利用正方形的性质及相应的三角函数得到点B的坐标.
分析:过点B向x轴引垂线,连接OB,可得OB的长度,进而得到点B的坐标,代入二次函数解析式即可求解.
解答:如图,作BE⊥x轴于点E,连接OB,
∵正方形OABC绕顶点O顺时针旋转75°,

∴∠AOE=75°,
∵∠AOB=45°,
∴∠BOE=30°,
∵OA=
 ,
,∴OB=2,
∴BE=
 OB=1,
OB=1,∴OE=
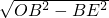 =
= ,
,∴点B坐标为(
 ,-1),
,-1),代入y=ax2(a<0)得a=-
 ,
,∴y=-
 x2x,
x2x,故选B.
点评:本题考查用待定系数法求函数解析式和勾股定理的运用,解题的关键是利用正方形的性质及相应的三角函数得到点B的坐标.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
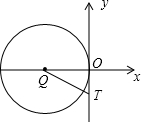
 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( ) (2012•集美区一模)如图,O为坐标原点,小明在运动场练习踢足球,足球在点O处飞出,落在点B处,已知足球经过的路线是抛物线
(2012•集美区一模)如图,O为坐标原点,小明在运动场练习踢足球,足球在点O处飞出,落在点B处,已知足球经过的路线是抛物线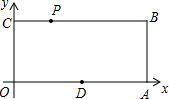 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动. 如图:0为坐标原点,点A(1,4)和点B(a,1)均在反比例函数
如图:0为坐标原点,点A(1,4)和点B(a,1)均在反比例函数