题目内容
16、下列有规律的两组数:
①2,4,6,8,10,12,…
②2,-6,12,-20,30,-42,…
(1)这两组数中的第8个数分别为
(2)分别写出这两组数中的第n个数(n为正整数,用含n的式子表示) 分别为_2n
(3)求这两组数中的第n个数的和(列式并化简)
①2,4,6,8,10,12,…
②2,-6,12,-20,30,-42,…
(1)这两组数中的第8个数分别为
16
和
-72
;(2)分别写出这两组数中的第n个数(n为正整数,用含n的式子表示) 分别为_2n
(-1)n+1n(n+1)
;(3)求这两组数中的第n个数的和(列式并化简)
(-1)n+1n(n+1)+2n
.分析:此题是数字规律题,要通过观察,分析归纳出两列数的规律.如第①列,发现每项的数是2×项数的得数.第②列,符号可以表示为(-1)n+1,然后再归纳数字之间的规律,进行解答.
解答:解:观察分析:①2,4,6,8,10,12,…
2=2×1,4=2×2,6=2×3,8=2×4,10=2×5,12=2×6,…?第n个数可表示为n×2即2n.
②2,-6,12,-20,30,-42,…
n=1时值为2×1 n=2时值为2×1+2×2 n=3时值为2×1+2×2+2×3,…依次类推 第n个数为 2×n+2×(n-1)…+2×2+2×1=2×(n+n-1+n-2…+2+1)=[2×(n+1)×n]/2=n(n+1). 前面的符号可表示为(-1)n+1,所以第n个数表示为:
(-1)n+1n(n+1).
那么,(1)这两组数中的第8个数分别为,2×8=16,(-1)8+1×8×(8+1)=-72.
故答案分别为:16,-72.
(2)这两组数中的第n个数(n为正整数,用含n的式子表示) 分别为:2n,(-1)n+1n(n+1).
故答案分别为:2n,(-1)n+1n(n+1).
(3)2n+(-1)n+1n(n+1)=(-1)n+1n(n+1)+2n.
2=2×1,4=2×2,6=2×3,8=2×4,10=2×5,12=2×6,…?第n个数可表示为n×2即2n.
②2,-6,12,-20,30,-42,…
n=1时值为2×1 n=2时值为2×1+2×2 n=3时值为2×1+2×2+2×3,…依次类推 第n个数为 2×n+2×(n-1)…+2×2+2×1=2×(n+n-1+n-2…+2+1)=[2×(n+1)×n]/2=n(n+1). 前面的符号可表示为(-1)n+1,所以第n个数表示为:
(-1)n+1n(n+1).
那么,(1)这两组数中的第8个数分别为,2×8=16,(-1)8+1×8×(8+1)=-72.
故答案分别为:16,-72.
(2)这两组数中的第n个数(n为正整数,用含n的式子表示) 分别为:2n,(-1)n+1n(n+1).
故答案分别为:2n,(-1)n+1n(n+1).
(3)2n+(-1)n+1n(n+1)=(-1)n+1n(n+1)+2n.
点评:此题要认真观察分析归纳两组数的规律,考查学生分析归纳问题的能力.解答的关键是第①列,发现每项的数是2×项数的得数.第②列要发现n=1时值为2×1 n=2时值为2×1+2×2 n=3时值为2×1+2×2+2×3,…依次类推 第n个数为 2×n+2×(n-1)…+2×2+2×1=2×(n+n-1+n-2…+2+1)=[2×(n+1)×n]/2=n(n+1).第②列数较难.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
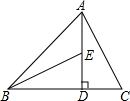
 。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则
。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则 ,这个结论就是著名的勾股定理.
,这个结论就是著名的勾股定理. 的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数

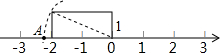
 的B点(保留作图痕迹).
的B点(保留作图痕迹).

 的B点(保留作图痕迹).
的B点(保留作图痕迹).